Tron BattleでLegend リーグ入りしたよ!
2023年10月02日 月曜日

CONTENTS
Tron Battleって知ってる?
突然ですが、Tron Battleって皆さん知ってますか?
昔ゲームであったようですが、今回の話はそれではありません。CodinGameというサイトで提供されているゲームで、ボットを自分でプログラミングし対戦するゲームの一つです。
CodinGameはコードゴルフやボットプログラミングで世界中の人々と対戦できるゲームがあります。web上で操作できるIDEが用意されていて、多数の言語にも対応しているため手軽に参加できます。Tron Battleはその中の一つです。
Tron Battleについて簡単に言うと、2~4人で行う限られた範囲で陣取り合戦をしながら生き残るゲームです。見た方がわかりやすいです。
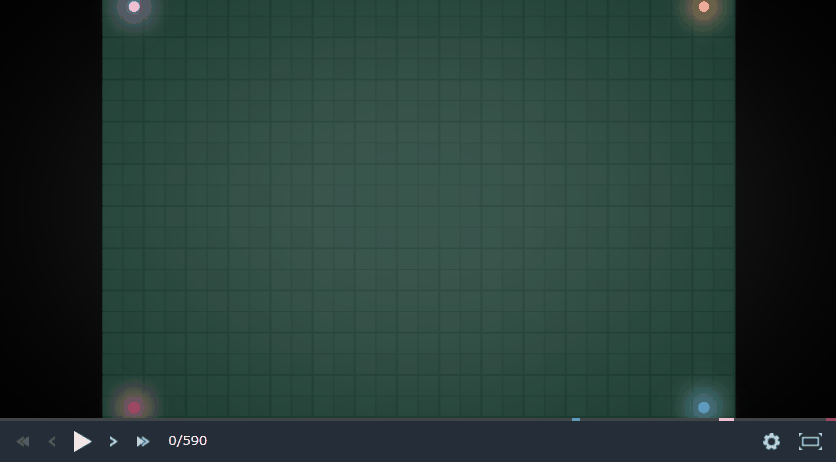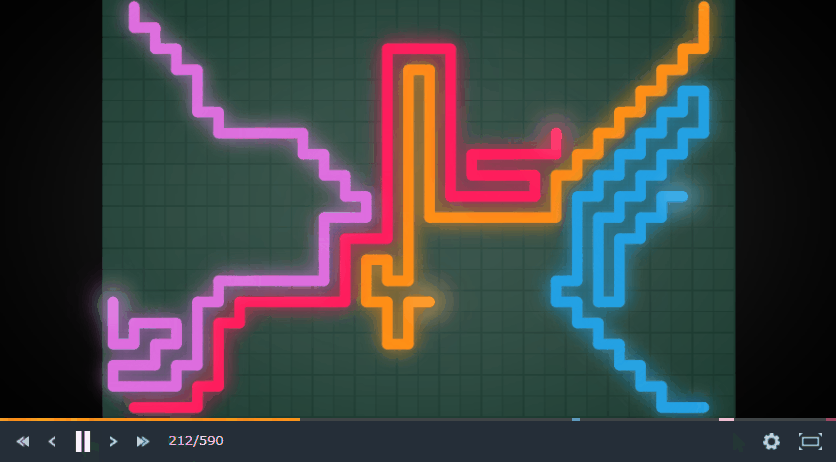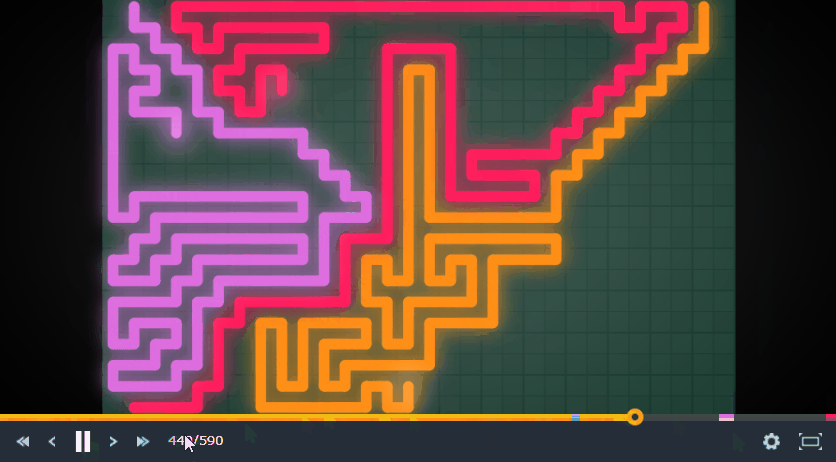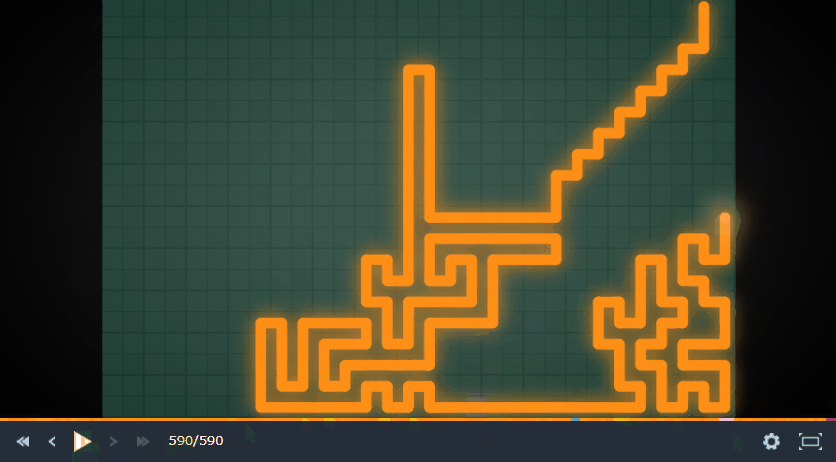
私はこのゲームでLegend リーグ入り、200位くらいまでいけました。今回は実装したボットについて書き連ねていこうと思います。
遅くなりましたが、はじめまして、うちやまです。普段はフロントエンドとサーバサイドのアプリケーション開発をしています。正直に言うとあまり業務に関係ない趣味でやっていたプログラミングについて書いていきます。そういう人もいるんだぁっということを知ってもらえるとうれしいです (ボットの中身に興味を持ってもらえたならもっとうれしいです)。
Tron Battleについて
ボットの中身を説明する前に、ゲームについて説明します。ルールなどは (英語ですが) CodinGameに書いてあるので、それを見る方がいいと思います。とはいえ、つらつらと書いていきます。
ゲームのルールは以下のようになってます。
- 30*20のボード上で戦う
- 各プレイヤーが順番に1マス移動しなければならない
- 上下左右しか移動できない
- 各プレイヤーが移動したマスには移動できない
- 負けたプレイヤーが移動したマスは、負けた後に解放される
- 移動できないマスに移動したか、バグがあったり計算に時間がかかったりなどで 一定時間を超えても移動できなかった場合、負け
- 最後まで残っていたプレイヤーが勝ち
上の動画を見ればわかりますが、各プレイヤーは1マスずつ移動しています。また、負けたプレイヤーの移動したマスは解放されます。
私たちはこのゲームのボットを作ります。具体的には入力データを受け取って、「LEFT、RIGHT、UP、DOWN」のいずれかを文字列で出力するボットを作ります。入力データの構造はこんな感じです。
- プレイヤー数 (2 ~ 4)
- 自分が操作するプレイヤーのID (0 ~ 3)
- プレイヤーごとに以下のデータを取得
- 初期位置の x、y 座標 (負けていた場合はどちらも -1)
- 現在位置の x、y 座標 (負けていた場合はどちらも -1)
CodinGameは親切で、各言語で入力データの読み込み部分は用意されています。なので、このターンで自分は「LEFT、RIGHT、UP、DOWN」のどの方向に1マス移動するかを実装するだけです。
ゲーム結果を次のゲームに引き継ぐことはできないので、強化学習などはできません。もちろん、ゲーム結果をダウンロードなどして活用することはできますが、ボットプログラミング内で強化していくことはできません。なので、いわゆるAIのようなものは作れません。 (シミュレーションなどはできますが、どこまでがAIというのか…)
Tron Battleはリーグがいくつかあります。下のリーグからWood、Bronze、Silver、Gold、Legendです。Legend以外はボスがいて、そのボスより強ければ上のリーグに行けます。強さはリーグ内で何度も対戦し、レートを計算して強さを比べてます。対戦は自動でやってくれるので、私たちが何かする必要はありません。対戦はリアルタイムか後からでも見れます。
Woodリーグ攻略 (グラフ理論と深さ優先探索、幅優先探索)
つらつらと前置きを書きましたが、ここからはボットの中身について書いていきましょう。
いきなりですが、皆さんはこのゲームをどう見ますか? このゲームは生き残れば勝ちです。では、どう生き残りますか?
簡単にするために、プレイヤーが自分だけと考えましょう。例えば、下のような状態になりました。Mが自分の位置です。青は自分が通ったマスで、オレンジは相手が通ったマスです。白は移動できるマスです。この場合、右と左に移動できますが、どちらに行きますか?
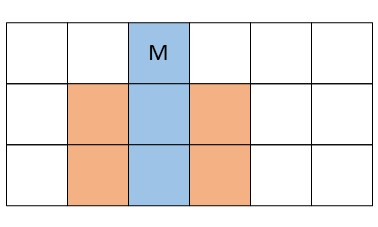
もちろん右に行きますよね? 右の方が広いですし。では、移動できるマス (今回は右or左) をどう調べますか? どうやって右の方がいいと計算しますか? プログラミングするとなると悩むのではないでしょうか?
こういう問題を考えるときによく使うのがグラフ理論です。グラフは頂点 (ノード) と枝 (エッジ) で表現されたもので、頂点同士を枝で結んだりします。(枝には向きがあることがあります。向きがある場合はリンクということがあります。)
さて、「皆さんはこのゲームをどう見ますか? 」ですが、私には下のようなグラフに見えてます。
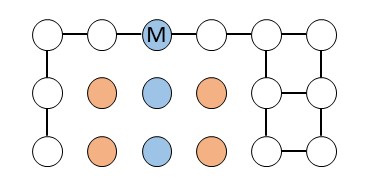
〇が頂点、-が枝です。頂点 (〇) がマス、枝 (-) が移動できる方向に対応します。色はわかりやすいようにつけてます。グラフで見ると、Mの頂点から出てる枝を見れば移動できる方向がわかり、白の頂点を数えれば広さがわかります。
このグラフを配列やリストに落とし込んでいろいろ計算していきます。データ構造については調べればいっぱい出てきます。Tron Battleは碁盤の目状なので、二次元配列で簡単に表現できます。
広さを計算するのは少し工夫が必要です。白の頂点を数えればいいだけではありません。移動できる頂点を数えないといけません。このときによく使われるのが深さ優先探索/幅優先探索です。どちらの探索も木を作っているのですが、移動できるマスを効率よく正確に計算できるとわかってもらえればここでは十分です。上のグラフを例に説明します。
迷路を攻略するときに右手で壁を触り続け、壁に沿って歩けばOKって話を聞いたことがありますか? それが深さ優先探索です。スタート位置から行けるところまで進み、そこから戻り別の方向へ行けるところまで進むことを繰り返して探索する方法です。一度通った頂点には進まないようにします。
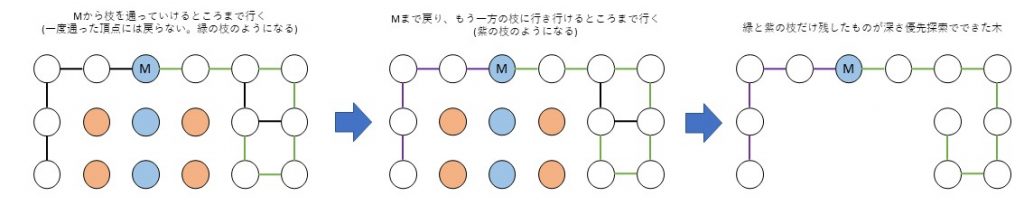
幅優先探索は現在地から行ける頂点を探す → 探した頂点から次に行ける頂点を探すことを繰り返して探索する方法です。一度通った頂点は探索しないようにします。
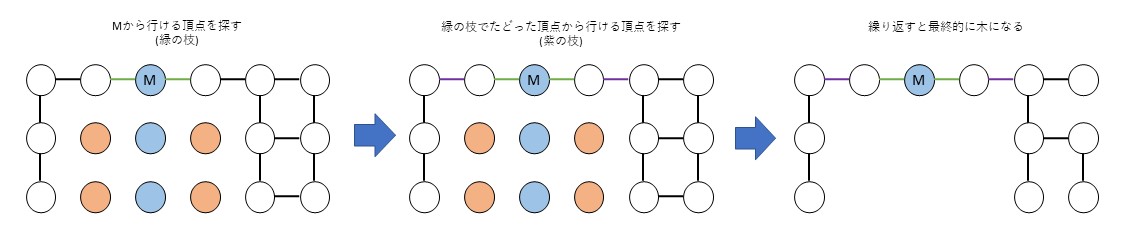
探索によってMから右or左に行ったときにどちらの方が広いのかがわかります。右に行ったときにたどれる頂点の個数と左に行ったときにたどれる頂点の個数を比較すればOKです。右は7個、左は4個なので右の方が広いです。深さ優先探索と幅優先探索の結果は違いますが、広さ (頂点の個数) は同じです。
グラフ理論と深さ優先探索/幅優先探索について話しましたが、深さ優先探索/幅優先探索で広い方に移動するボットは強いです。余裕でWoodリーグは突破できます。
Bronzeリーグ攻略 (ボロノイ領域)
深さ優先探索/幅優先探索でより広い領域を見つけることができました。でもこれは本当に広いですか ?
以下のような状態を考えます。白が移動できるマスです。プレイヤー P と Q が移動できそうな領域ってどのくらい変わるでしょうか ?
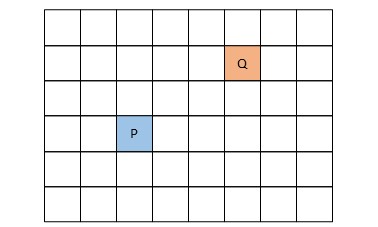
深さ優先探索/幅優先探索の場合、PもQも上下左右どこに移動しても広さは同じです。ですが、Tron Battleは対戦ゲームなので、どちらかのプレイヤーが移動すれば移動できるマスは減っていきます。さらに、自分からより遠いマスを使えることはほぼないでしょう。つまり、深さ優先探索/幅優先探索で見つかった移動できるマスは、将来移動できるかどうかまではわかりません。ほとんど移動できない可能性もあります。
では、自分が移動できそうなマスはどう見つければいいでしょうか?
ぱっと思いつくのは距離です。あるマスへの最短距離が一番近いプレイヤーがそのマスへ移動できそうです。例えば、下のSのマスへはPが3マスの移動、Qが4マスの移動で到着するので、Pの方がSのマスを使えそうです。
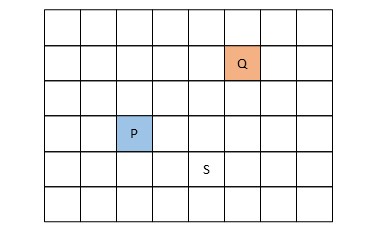
このように考えていくと、PとQが移動できそうなマスは下のようになります。
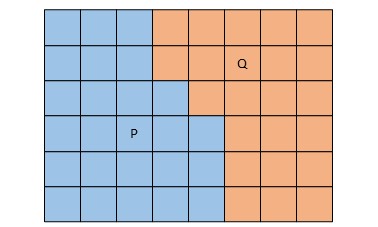
今いる位置を除いて、Pが移動できそうなマス (青のマス) は24マス、Qが移動できそうなマス (オレンジのマス) は22マスで、Pの方がおそらく有利でしょう。
この考えを取り入れていきます。このターンに移動できるマスにそれぞれ移動し、上の方法で移動できそうなマスを計算し、一番移動できそうなマスが多い方向に移動します。Pが上下左右それぞれ移動すると下のようになります。
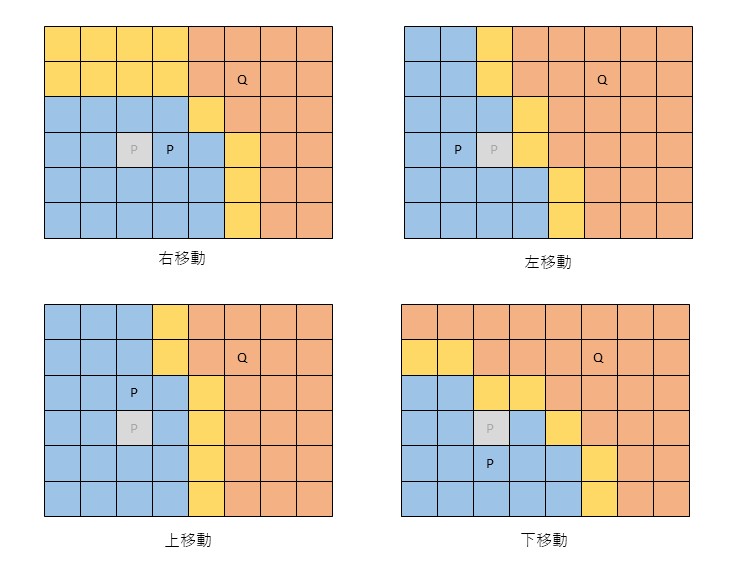
黄色のマスはPとQから等距離にあるマスです。黄色のマスは先行するプレイヤーが移動できるマスなのですが、ややこしいので今回は無視します (実際は無視すると強さが変わってくるのでちゃんと考えます)。移動前のマス (灰色のマス) には移動できないので注意してください。青のマスをそれぞれ数えると、右移動時は18マス、左移動時は17マス、上移動時は21マス、下移動時は15マスとなり、上に行くのが一番よさそうです。
さて、考え方は話しましたが、このような領域をボロノイ領域 (ボロノイ図) といいます。平面上にあるいくつかの点 (母点といいます) の中で、どの点 (母点) に一番近いかで平面を分けた図のことです。図を見た方がわかりやすいです。
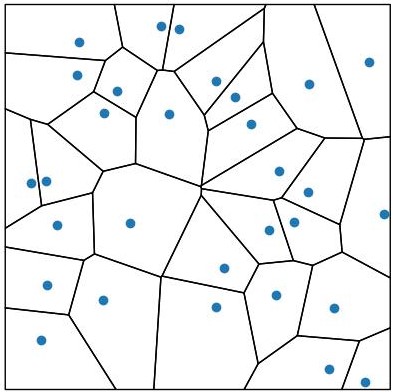
青の点が母点になります。ドロネー図の双対って話もありますが、興味ある人は調べてみてください (私はそっち方面には全く詳しくないです)。聞きなじみがないかもしれませんが、キリンの模様やトンボの羽の模様などはボロノイ図になってるようです。いろいろな場面でボロノイ図が現れたり使われたりしているので、実は見たことあるかもしれません。
ボロノイ領域を求めるのは大変だったりします。Pythonなら簡単ですがCodinGameでパッケージがどこまで使えるかはわかりません。しかし、Tron Battleは碁盤の目状なので簡単に計算できます。ダイクストラ法すらいりません。実は幅優先探索が最短距離を求めるアルゴリズムとして使えます。
このボロノイ領域を用いて移動方向を決めるボットは結構強くてBronzeリーグは軽く突破します。Silverでも通用します。
Silverリーグ攻略 (ゲーム木)
ボロノイ領域を使ったボットはかなり強く、Silverリーグでも100~120位くらいまで行けました。しかし突破はできません。
対戦ゲームのAI (ボット) でよく見るのがゲーム木です。これを取り入れていきます。人間は次の手を読んであーだこーだと考えますが、ゲーム木はその人間の思考を実装したものです。強いAIは盤面を正確 ? に評価できるのですが、盤面の評価はかなり難しく職人技のようなものなので最初はやりません。計算力のゴリ押しで全パターン考えていきます。
単純なゲーム木を取り入れていきます。全プレイヤーを1マス移動させ、最後の盤面でボロノイ領域を計算します。各プレイヤーは計算したボロノイ領域をみて一番広くなる方へ移動をします。例えば、2人対戦で各プレイヤーは3方向 (UP、DOWN、RIGHT) に移動できるとすると、ゲーム木はこのようになります。
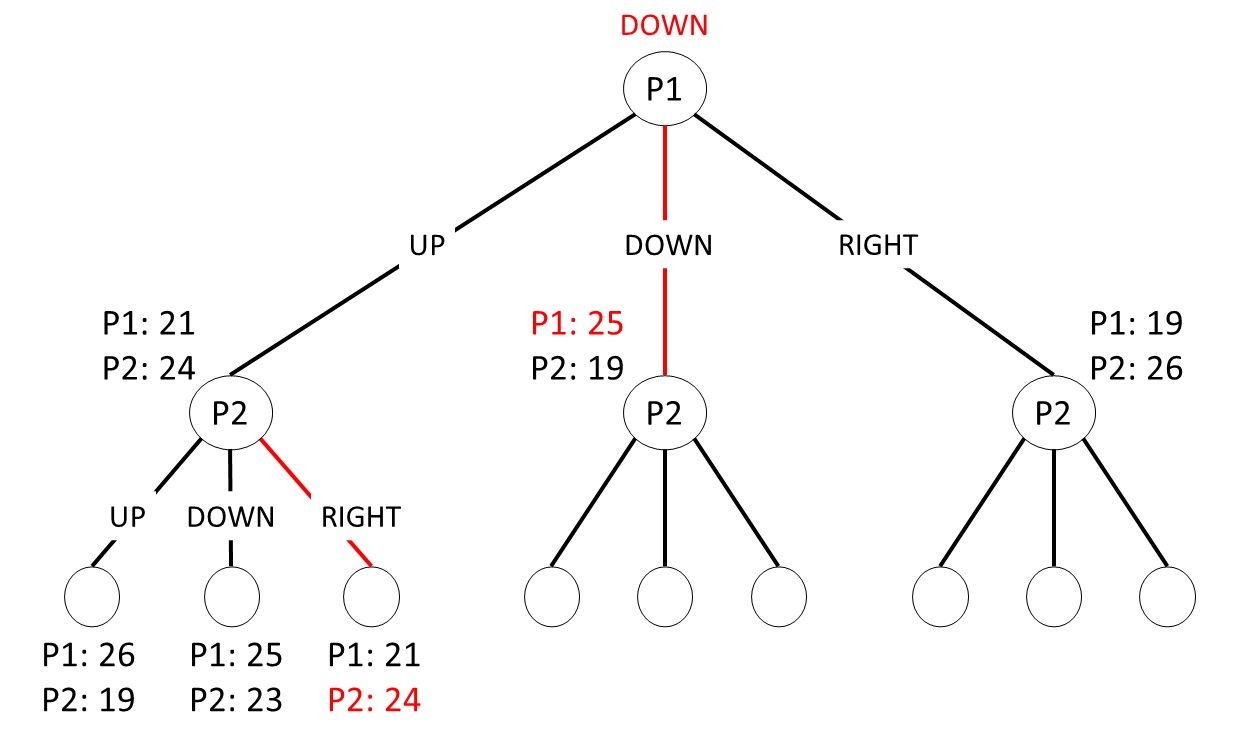
2プレイヤーでそれぞれ3通りの手しかありませんが、盤面は全部で8通りあります。本筋からそれますが、ゲーム木はプレイヤーや手の多さが多くなるほど、読む深さが深くなるほど爆発的に盤面の数が増えます (組み合わせ爆発といいます)。深く読めば強いですがとても時間がかかります。だから難しく、みんな効率化や盤面の評価でかなりの工夫を入れます。
話は戻って、ゲーム木は頂点 (〇) と枝 (-) でできているのでグラフで、木 (tree) といわれるものです。木は頂点間を枝を伝って移動可能で、枝を伝ってもスタートの頂点に戻ってこれないグラフのことです (深さ優先探索/幅優先探索で求めたものも木です)。木 (ゲーム木) の一番上の頂点を根 (root) といい、一番下の頂点を葉 (leaf) といいます。上の図の場合、一番上の P1 が根、一番下の何も書いてない頂点が葉です。頂点は各プレイヤーのターン、枝は各プレイヤーの移動を表しています。根で自分 (P1) がどの方向に移動すればいいのかがわかり、葉でボロノイ領域を計算して盤面を評価していきます。各頂点でボロノイ領域を計算しません。葉だけです。
頂点のそばに「P1: 26, P2:19」などがありますが、これはその盤面での各プレイヤーのボロノイ領域の広さ (マスの数) を表しています。例えば、左下の
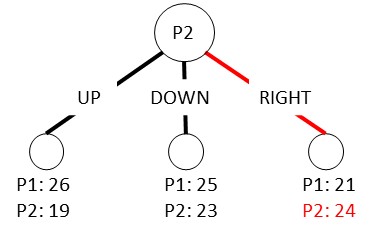
は、プレイヤー2 (P2) の手を考えています。葉を見るとRIGHTが一番広い (24マス) なのでP2はRIGHTを選びます。これを葉から繰り返して上に伝播させていくと、根のP1はDOWNが選ばれます。
ゲーム木は再起関数を使うと楽に実装できます。ゲーム木をボットに取り入れたらSilverリーグは突破できました。
Goldリーグ攻略 (最長経路)
ゲーム木は深く読むほど計算に時間がかかります。CodinGameのタイムアウトは100ミリ秒なので、実は深く読めません。とはいえ、ゲーム木をチューニングしたりボロノイ領域を効率よく計算すればGoldリーグでも100位まで行けます。並列化などでもっと頑張ればGoldリーグを突破できそうですが、ここでは別のアプローチを選びました。
Tron Battleは対戦ゲームですが、他のプレイヤーの動きに全く影響しない場面がかなりあります。こういう場面です。

各プレイヤーが閉鎖された領域にいます。このとき、プレイヤーが動いてもボロノイ領域は変化しないので、ボロノイ領域に意味ありません。移動できるマスをなるべく多く使って生き残ることが重要です。
これが簡単に見えるかもしれませんが、案外難しいです。
整理すると、マスを1度しか使えない制約で一番長い一本道を探したいです。グラフ理論では頂点と枝を交互に選んだものを経路 (もしくは歩道) といい、同じ頂点を選ばない経路を道 (path) といいます。この辺はややこしい言葉の定義なのでフーンっと思ってもらえれば十分です。今回探したいのは最長のパス (道) で、この問題が非常に難しく、NP-困難と言われる問題です。
普通に探しても難しく、タイムアウトもあるので最長パスを計算するのはほぼ無理です。こういうときにとられる方法は大きく3つあります。
- 局所探索、ヒューリスティックを使う
- 最もいい解ではないが、最悪 (もしくは経験的に) このくらいの悪さの解が求められる簡単な方法を作る
- 愚直に探索し、探索で効率化をはかる
それぞれ学術的に一分野を築いてるもので、とっても深い内容になってます。競プロとかでよく聞くのは局所探索、ヒューリスティックで、遺伝アルゴリズムやアニーリング法 (焼きなまし法) がこれに当たります。二つ目の内容と組み合わせて使う場合もあります。三つ目はほとんど聞きません。三つ目でできるならそれは知っていれば解ける問題なので、競プロなどの問題として採用されないと思います (理論的にはとっても難しく興味深いのですが)。
今回は局所探索を利用します。タイムアウトがあるので遺伝アルゴリズムやアニーリング法などの高尚なものは使いません。原始的に行きましょう。
局所探索の考えはシンプルで、答えを適当に作って、答えを変形してよさそうな答えができたらまた変形ということを繰り返していきます。経験的かどうかは自信ないですが、いい解の周りによりいい解があること多いことが知られてます。局所探索はいい解の周りを重点的に調べつくしてよりいい解を探すというのが根底にあります。
種類も様々あり、遺伝アルゴリズムやアニーリング法はいい解の作り方や更新条件に工夫を入れて、よりいい解を探す方法になってます。単純な局所探索というと、探索していきいい解がなければ終わりという方法になります。これではさすがになので、探索が終わったら最初からやり直す探索方法 (多スタート法) を使います。
具体的に言うと、以下のようなアルゴリズムを使います。
- 今いる位置から移動できる方向を探す
- 1 で移動できる方向がないなら終わり。パスを覚えておき、はじめからやり直す
- 1 で移動できる方向があるなら、ランダムでどれかの方向に動く
- 1 に戻る
これを時間いっぱいまで行い、計算で得られた最長パスから移動方向を決めます。要はランダムウォークして最長パスを探してます。
これで本当によくなるのが局所探索の面白いところです。実際には工夫をいくつか入れてますが、非常にうまく動きます。このアルゴリズムを取り入れたボットの動きを見てください (黄色がそのボットです)。
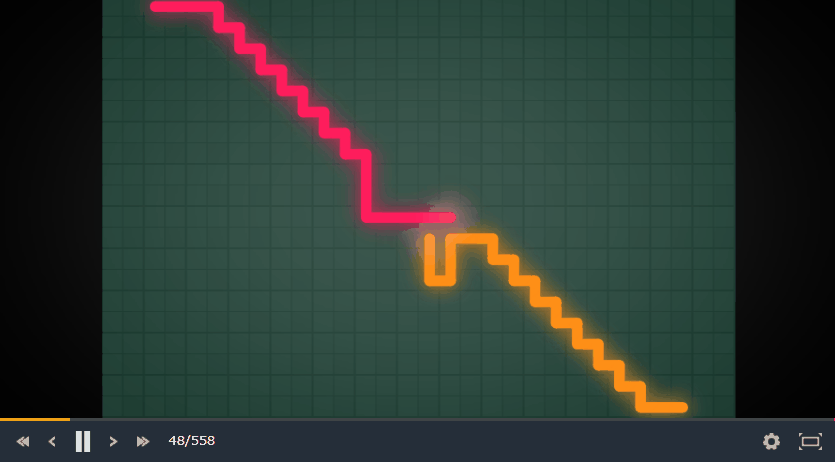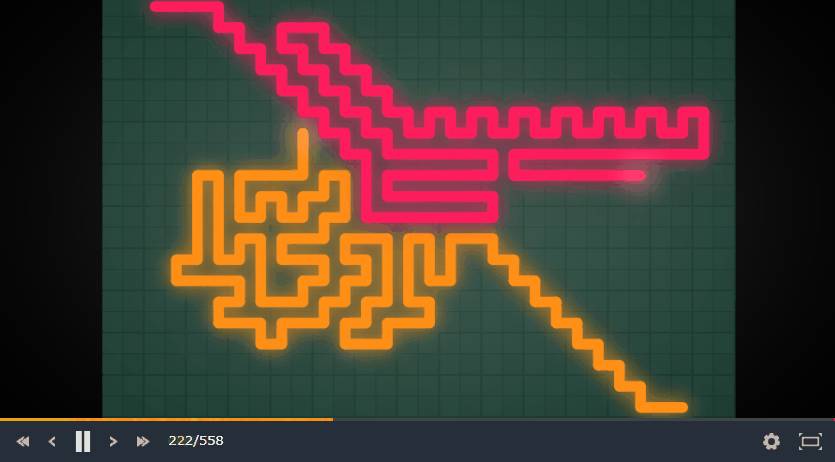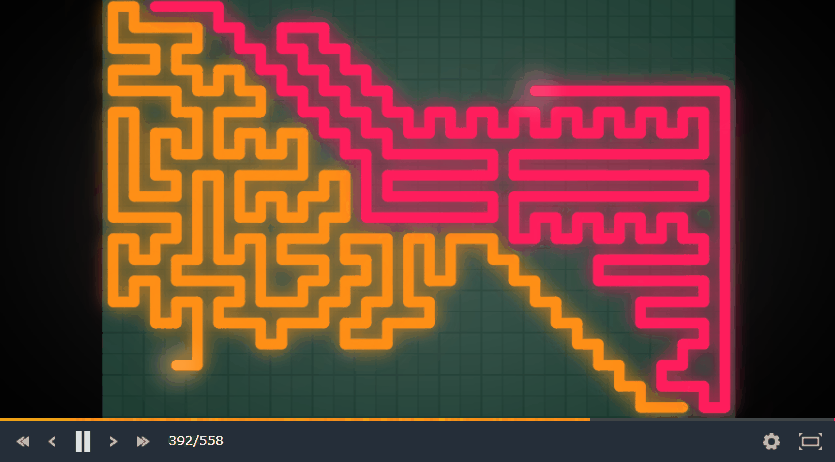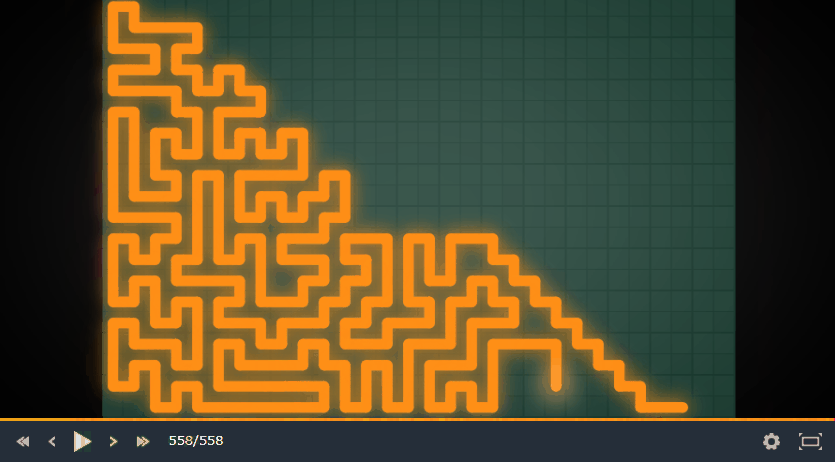
動きが気持ち悪いですが、かなりよくマスを使い切れてると思います。
このアルゴリズムを取り入れてGoldリーグは突破できました。
Legendリーグ (評価関数とAlpha-Beta法)
Goldリーグ突破時のボットでは420~450位になりました。ここからが大変です。
ゲーム木を作り、最長パスをどうにかして求めて効率よくマスを使い切ってます。普通に強いのですが、Legendリーグの人たちは本当にレジェンドです。ここで修正したり取り入れたりした内容は細かかったり難しかったりするので、大きい変更を1つ紹介します。
より強いボットを作るために、Tron Battleについて理解を深めましょう。
ボロノイ領域を各プレイヤーごとに計算してましたが、ここをもっと考えていきます。重要なのは自分のボロノイ領域で、自分の領域が大きくなれば他のプレイヤーの領域は小さくなっていきます。なので、盤面の評価で以下のことを考えていきます。
- 自分のボロノイ領域の大きさ (マスの数)
- 相手のボロノイ領域の大きさ (マスの数) が自分のものに比べてどのくらい大きいか
この2つの和で盤面を評価していきます。
ゲーム木の説明で、各頂点でプレイヤーは自分のボロノイ領域が一番大きい方向に動いてましたが、この選択方法を変えます。自分のターンでは上の評価の和が大きいもの、相手のターンでは上の評価の和が一番小さいものを選択するように移動していきます。つまり、上の評価の和について自分は最大に、相手は最小にしようとして動きます。
このようにすることで、ゲーム木の探索を効率化することができます。Alpha-Beta法といわれるものです。詳しくは書きませんが、得られた暫定解を利用して不要な手の読み (探索) を省こうというものです。
他にも工夫を取り入れ、200~220位まで行けました。
最後に
最終的にはLegend リーグの200~220位くらいまでいきました。
探索を効率的にしたり並列処理をさせたり、評価関数を変えたり、動ける領域が少なくなったときに勝てる動きをハードコードしたりなど、まだまだいろいろ試したかったのですが、力尽きました。
グラフ理論や最適化は好きになれましたか? 私は大好きです。
ネットワーク自体がグラフ理論の一部なので、通信分野でもたまに見かけるものがあるかもしれません。グラフ理論から生まれたアルゴリズムなんかは通信分野で使われています。ダイクストラ法が有名ですね。
文献が書いてありませんが、そこは申し訳ないです (どれを文献にすればいいのかという。私の実力が足りない)。とはいえ、ここで書いてある内容は数えきれないくらい書いてあります。興味があれば見てみてください。競プロから調べてみるのも面白いですよ。
実問題はとっても難しいので、大学などで学んだことをそのまま使えません。でも、学んだことを組み合わせれば案外いろいろなものが解けたりします。実問題にも抗えたりします。今回紹介したものはよく見かけるものなので、知ってる人もいると思います。それらを組み合わせると、よりすごいことができることを感じてくれたらうれしいです。興味あれば手を動かしてみてください。「なんでそうなるんだ!」とか「あれ? 案外弱い?」とかとか、もっと面白くなりますよ。







