シェルスクリプトで雪の結晶を描く
2024年12月05日 木曜日

CONTENTS
【IIJ 2024 TECHアドベントカレンダー 12/5の記事です】
はじめに
アドベントカレンダーなのでクリスマスっぽいことをしましょう。ホワイトクリスマスには雪。ということで、六角形の雪の結晶の絵を描くスクリプトを書きます。
注意: この記事ではスクリプトの例をいくつか挙げますが、まともな人間が解読できるものは出てきません。真面目に読もうとすると目が腐ります。まともなプログラムは生成AIに任せて、人間は生産性を/dev/nullに捨てるスクリプトを書くことに全力を注ぎましょう。必要な情報は文中のリンク先を参照することで得られるようにしてありますので、コードは無視してそちらを参考にしてください。
ドット絵を描く
コンピュータで絵を描くには、まず画像フォーマットを知る必要があります。
ドット絵を描くのは難しくありません。たとえば、白黒2値画像ならばこんなファイルを用意しましょう。
P1 20 20 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
ただのテキストデータですが、これでもPBM (portable bitmap)という立派な画像形式です。
先頭2行はヘッダです。P1はPBM(ascii)の画像であることをあらわし、20 20は画像の幅x高さです。3行目以降は、見ればわかると思いますがドット絵をゼロとイチで並べただけです。
この例は白黒2値ですが、グレイスケール(PGM; portable graymap)やカラー画像(PPM; portable pixmap)も同じような方法で作成でき、総称して PNM(portable anymap)と呼ばれます。PNM形式の詳しい解説はたとえばWikipediaを見てください。
PNMはひじょーに簡単な構造なので、お手製のスクリプトで画像を扱うのに適しています。この形式で出力できれば、あとはImageMagickのconvertというコマンドで一般的な画像形式に変換してやればおっけーです。
convert A.pbm A.gif
こんな画像が得られます。
![]()
カンタンですね。こんなふうにドット絵を出力するスクリプトを書けばいいのです。
ちなみに、このPBM形式のテキストデータはドットをぽちぽち手打ちしたわけではなく、以下のコマンドを実行して得られたものです。画像形式のひとつなので、画像として生成するのがてっとりばやいです。
convert -size 20x20 xc: -gravity center -pointsize 24 -draw 'text 0,0 "A"' -compress none A.pbm
反復関数系でコッホ曲線を描く
それでは雪の結晶の絵を描きましょう。
雪といえばもちろんコッホ雪片です。
線分を3等分し、その真ん中の2点を頂点とする正三角形を描く、という操作を無限に繰り返すことでできるフラクタル図形がコッホ曲線であり、それを3つつなぎあわせたものがコッホ雪片です。
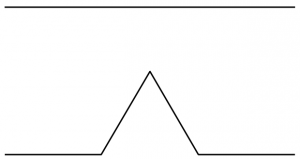
このコッホ雪片を描きましょう。いろいろ方法はありますが、まずは反復関数系(IFS)というアルゴリズムでドットを打っていきます。
あらかじめ用意した複数の関数群の中からどれかひとつをランダムに選んで座標(x,y)に適用し、その結果を新たな座標とする、という操作を何度も繰り返すと、なぜかフラクタルな図形を生成できてしまう、というのがIFS。なんでそうなるのか筆者は理解してないので、これ以上の解説はできません。Wikipedia先生を見てください。
とりあえず、Wikipediaのコッホ曲線#コンピュータによる生成がまさにIFSによる描画方法です。詳しいことを理解してなくても、ここに書いてあるとおりスクリプトを書けばおっけーです。
echo 400 | awk 'END{p=1/3;q=1/6;r=12^-.5;for(split(p" 0 0 "p";"q" -"r" "r" "q" "p";"q" "r" -"r" "q" .5 "r";"p" 0 0 "p" "2/3,f,";");++i<1e5;){$0=f[int(rand()*4)+1];z=$1*x+$2*y+$5;y=$3*x+$4*y+$6;x=z;t[int(x*a)+int(y*a)*a]=1}for(j=a*a*.3;j;)print+t[--j]}$0="P1 "(a=$1)" "a*.3' | convert - koch1.png
awkのワンライナーで書けました。簡単ですね。冒頭のecho 400は画像の横幅で、この値を変えるといろんな画像サイズのコッホ曲線を描けます。
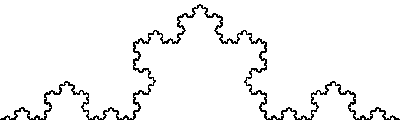
これをてきとーに回転させたものを3つくっつければ、コッホ雪片になります。画像の回転や結合はImageMagickの得意とするところなので、そちらにまかせましょう。上のワンライナーの最後のconvertコマンドを以下のように変えればおっけーです。
... | convert - \( +clone -rotate 240 \( +clone -flop \) +append -trim \) -append koch2.png
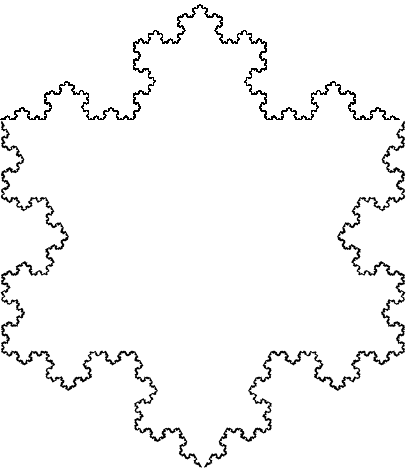
ということで、コッホ雪片を描くごとができました。
線画を描く
絵を描く方法はドットを打つだけではありません。昔むかしBASICでLINE文やCIRCLE文といった命令を駆使して絵を描いていたおじさんもいるんじゃないかと思います。それと同じようなことができればいいですね。はい、ImageMagickでできます。
たとえば、以下のコマンドは直線3つで描いた三角形を出力します。
convert -size 300x300 xc: -draw 'fill none stroke black line 150,20 0,280 line 0,280 299,280 line 299,280 150,20' triangle.gif
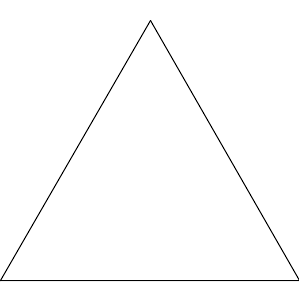
L-systemでコッホ雪片を描く
「線分を3等分し、その真ん中の2点を頂点とする正三角形を描く、という操作を無限に繰り返す」のがコッホ曲線です。これの見方を変えると、ある線分を「線分/左に60度方向転換/線分/右に120度方向転換/線分/左に60度方向転換/線分」に置き替える操作を無限に繰り返す、ということです。
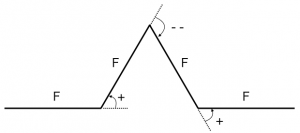
ここで、線分をF、左右に60度の方向転換をそれぞれ+、-で表記することにすると、
F -> F+F--F+F
という置換操作を無限に繰り返せばいいことになります。このアルゴリズムをL-systemと呼びます。
この方法では座標を絶対位置で指示するのではなく、まっすぐ進んで左に曲がってまたまっすぐ進んで、……という現在地からの距離と方向を相対位置で指示して絵を描くことになりますが、これはまさにタートルグラフィックスです。そして、ImageMagickにはタートルグラフィックスっぽいことをやるのに都合のよいディレクティブが存在します。ということで、タートルがどう動くべきかの命令をL-systemで生成し、それをImageMagickのディレクティブに変換してやればいいですね。
この記号による表記では、正三角形は F--F--Fで表されます。ということで、正三角形からスタートしてL-systemの置換操作を無限回おこなう……のは無理なので適当な回数だけおこなってImageMagickに描かせるスクリプトを書いてみましょう。文字列の置換が主になるので、置換を得意とする言語、そう、マクロプロセッサのm4が適任ですね。
divert(-1) define(`Lsystem',`ifelse($2,0,,`Lsystem($1,decr($2),$3)')define($3,`$1')') define(`F',``F L F R R F L F'') // m4の仕様の都合上、+-のかわりにLRを使う Lsystem(`F R R F R R F',5,`_path_') define(`dir',`ifelse($1,0,``2,0'',$1,1,``1,-2'',$1,2,``-1,-2'',$1,3,``-2,0'',$1,4,``-1,2'',``1,2'')') define(`i',0) define(`F',`dir(i)') define(`L',`define(`i',eval((i+1)%6))') define(`R',`define(`i',eval((i+5)%6))') syscmd(`convert -size 500x670 xc:black -draw "fill white path ''`m5,170 '_path_`''`" koch3.png') divert(0)dnl
実行結果。

きれいな雪の結晶ができました。
さらに、線分を置き換える折れ線の真ん中に逆三角形をくっつける、つまりF -> F+F--F+Fという置換操作のうち--の部分を+F--F--F+に変更し、六角形(F+F+F+F+F+F)から開始するとヘキサフレークというフラクタル図形が得られます。複雑になってはいますがいたるところにコッホ雪片が見られますね。
divert(-1) define(`Lsystem',`ifelse($2,0,,`Lsystem($1,decr($2),$3)')define($3,`$1')') define(`F',``F L F L F R R F R R F L F L F'') Lsystem(`F L F L F L F L F L F',4,`_path_') define(`dir',`ifelse($1,0,``2,0'',$1,1,``1,-2'',$1,2,``-1,-2'',$1,3,``-2,0'',$1,4,``-1,2'',``1,2'')') define(`i',0) define(`F',`dir(i)') define(`L',`define(`i',eval((i+1)%6))') define(`R',`define(`i',eval((i+5)%6))') syscmd(`convert -size 350x350 xc: -draw "fill none stroke black path ''`m95,335 '_path_`''`" hexaflake.png') divert(0)dnl

ギャラリー
PNMの画像フォーマットと、ImageMagickのdrawディレクティブ、この2つを知っていれば、いろんな絵をスクリプトで生成することができるようになります。ということで、雪の結晶以外にもいくつか例を挙げてみましょう。
Barnsley fern
IFSはコッホ曲線を描くためにあるものではなく、汎用性のあるものです。以下はコッホ曲線のスクリプトと中身はほぼ同じ、パラメータを変えただけのワンライナーです。
awk '1;{for(;i++<3e4;x=z){r=rand()*100;$0=r<1?.16:r<8?".24 -.15 .28 .26 .44":r<93?".85 .85 .04 -.04 1.6":".22 .2 -.26 .23 1.6";z=$2*x+$3*y;y=$4*x+$1*y+$5;t[int(y*50)*400-int(z*50)-1e3]=1};for(j=2e5;j--;)print+t[j]}'<<<"P1 400 500" | convert - +level-colors green,black fern.png

実行すると、なぜかシダ植物が描画されてしまいました。Barnsley fernというそうです。
ドラゴン曲線
L-systemもまた汎用的なものです。以下のm4マクロはパラメータ以外はコッホ雪片とまったく同じものです。
divert(-1) define(`Lsystem',`ifelse($2,0,,`Lsystem($1,decr($2),$3)')define($3,`$1')') define(`X',``X L Y F L'') define(`Y',``R F X R Y'') Lsystem(`F X',13,`_path_') define(`dir',`ifelse($1,0,``1,1'',$1,1,``1,-1'',$1,2,``-1,-1'',``-1,1'')') define(`i',0) define(`F',`dir(i)') define(`X',`dir(i)') define(`Y',`dir(i)') define(`L',`define(`i',eval((i+1)%4))') define(`R',`define(`i',eval((i+3)%4))') syscmd(`convert -size 400x280 xc: -draw "stroke black fill none path ''`m305,185 '_path_`''`" dragon.png') divert(0)dnl

フラクタル図形のひとつ、ドラゴン曲線があらわれました。
ペンローズタイル
非周期平面充填図形であるペンローズタイルもL-systemで描けます。こちらはbashで書いてみました。ImageMagickが一度に扱える上限以上の線を描画するためにかなりトリッキーなことをやってます。
eval 'p=$(sed "s/M/oA++pA----nA<-oA----mA>++/g;s/N/+oA--pA<---mA--nA>+/g;s/O/-mA++nA<+++oA++pA>-/g;s/P/--oA++++mA<+pA++++nA>--nA/g;s/A/\n/g;y/mnop/MNOP/"<<<${p=<N>++<N>++<N>++<N>++<N>});'{,,,,,,}
eval $(sed 's/[-+]/((i&&));/g;s/[MNOP]/echo stroke $& line $X,$Y $[X+=x[i%10]],$[Y+=y[i%10]];/g;s/</S[++s]=\"X=$X;Y=$Y;i=$i\";/g;s/>/eval ${S[s--]};/g;1i\
x=(10 8 3 -3 -8 -10 -8 -3 3 8);y=(0 6 10 10 6 0 -6 -10 -10 -6);X=300;Y=300;M=red;N=blue;O=green;P=purple'<<<"$p" | bash | awk '($4$5 in a)?0:++a[$4$5]' | xargs -n1000 | sed 's/.*/convert - -draw "fill none &" ppm:- |/;1i\
convert -size 600x600 xc: ppm:- |
$a\
convert - penrosetile.png')

マンデルブロ集合
ここまでフラクタル図形をいくつか描いてきましたが、フラクタルといえばやっぱり、式自体はめちゃくちゃ簡単なのに生成される画像はめちゃくちゃ複雑というマンデルブロ集合ですね。逆ポーランド電卓のdcによるワンライナーです。
dc -e'_2 _1.5 3 64 512 sSsDsWsYsXlD1-lSd[P2]f[lxd*lyd*-la+2lxly**lb+sysxlj1-dsj0!=tlj]sz[lxd*lyd*+4>z]st[0klilS~16klW*lS1-/lX+salS-_1*lW*lS1-/lY+sb0dsxsylDsjlzxpli1+dsilSd*!=m]sm0silmx'|convert - mandelbrot.png

先頭に並んでる数字のうち3つは計算する複素平面の範囲で、_2 _1.5 3は (-2-1.5i) - (-2+3+(-1.5+3)i)を描画します(_は負号です)。その次の64は収束と判断して繰り返しを打ち切るまでの回数(兼グレイスケールの階調)、512は画像サイズです。たとえば値を _0.708 0.284 0.045 256 512 に変えて実行してみると以下のような画像が得られます。

ライフゲーム
平面上のあるマスとその周囲8マスの状態によって、そのマスの次の世代の生死が決定される、というのがライフゲームです。
このスクリプトに標準入力からてきとーな画像を食わせると、その画像を白黒2値化したものをライフゲームの初期状態とみなし、その後の100世代(引数で変更可)をアニメーションgifとして出力します。デカい画像でやるとめっちゃ時間がかかるので注意。
#!/bin/bash
gen=${1-100}
convert - /tmp/$$_0000.gif
trap 'rm /tmp/$$_????.???' EXIT
eval $(convert /tmp/$$_0000.gif -compress none pbm:- | sed '/^#/d' | xargs | sed '1s/P1 \([^ ]*\) \([^ ]*\) \(.*\)/W=\1;H=\2;L=($(tr -dc 01 <<<"\3/;$s/$/"|fold -$W))/')
while ((g++<gen));do
M=($(echo ${L[@]} | xargs -n1 | sed 's/\(\(.\).*\(.\)\)/\3\1\2/'))
L=()
i=$H
while ((j=0,i--)); do
while ((j<W)); do
((t=${M[i]:j+1:1}*10+9${M[(i+H-1)%H]:j:3}${M[i]:j:3}${M[(i+1)%H]:j++:3}%9,(t-3)*(t-13)*(t-14)))
L[i]+=$?
done
done
{ echo P1 $W $H; echo ${L[@]} | sed 's/./& /g';} > $(printf /tmp/$$_%04d.pbm $g)
done
convert -delay 50 -loop 0 -layers optimize /tmp/$$_????.??? gif:-
この記事に出てくるスクリプトの中ではもっともわかりすいでしょう。ループのいちばん深いところ、次の世代の生死を判定する部分を除けば。
実行例。こちらの画像を使いました。
% bash lifegame.sh < bp-barry-kun-150px.png > barry.gif

シェルピンスキーのギャスケット
これまたフラクタルの代表格、シェルピンスキーのギャスケットです。
先ほどのライフゲームは「平面上のある点とその周囲の点」によって次の世代の状態が決定されます。これは二次元セルオートマトンとしてモデル化されます。そして、平面ではなく「直線上のある点とその周囲の点」により次の世代が決定されるとしたものが一次元セルオートマトンです。このシェルピンキーのギャスケットは、一次元セルオートマトンのRule 90により描画しています。
! _(){
((____=__,${_______=_____[____]^=_____[____-__],++____<___&&_______}))
$______<<<${_____[@]}
((++________<___))&&_
}
_____=(${__=$?})
___=$[__<<$__$?-__]
: /*/$$;: ${_:__:__}
(${______=/???/???/?$[~__*~__]}<<<${_^}$__\ $___\ $___;_)|convert - -rotate 45 -trim sierpinski.png

記号ばっかりですが、bashスクリプトです(ashやdashは不可)。/usr/bin/m4がインストールされているLinuxでないと動きません(procfsをマウントしておけば*BSDでも動きます)。
おわりに
コツさえ知っていれば、スクリプトで絵を描くのは難しくありません。この記事で挙げたようなフラクタル図形をお仕事で描くことはまずないかと思いますが、プログラムで画像を加工・生成する方法を知っておくと、大量の画像処理をするのに専用のアプリで1枚ずつ処理したりする手間をかけずに済みます。この記事ではあえてなじみの薄い言語を使いましたが、もちろん他の言語でもおっけーです(というかまともな用途でこんな言語を使うのはやめましょう)。いろいろ工夫して遊んでみるとよいかと思います。

Xのフォロー&条件付きツイートで、「IoT米」と「バリーくんシール」のセットを抽選でプレゼント!
応募期間は2024/12/02~2024/12/31まで。詳細はこちらをご覧ください。
今すぐポストするならこちら→![]() フォローもお忘れなく!
フォローもお忘れなく!





![「[IIJ Bootcamp] ハンズオン研修2021 開催報告」のイメージ](https://eng-blog.iij.ad.jp/wp-content/uploads/2020/11/a11b4bb3ba448d1fa402ac3dc62cc91f-300x169.png)
