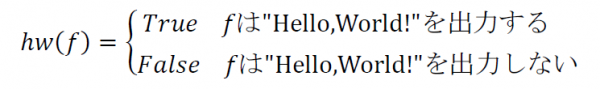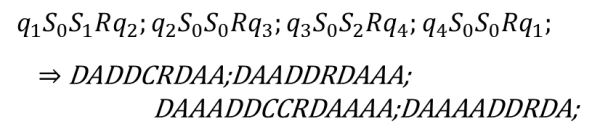チューリングの停止性問題
2019年07月01日 月曜日

Contents
本記事は別途PDFでもご用意しており、こちらよりダウンロードいただけます。
Disclaimer:このエッセイは独自解釈を多数含むが,著者は計算理論を専門に学んだことはないため,いくつかの点で不正確な可能性がある
0.イントロダクション
この短いエッセイでは1936年のチューリングの記念碑的な論文である『計算可能数とその決定問題への応用(“On Computable Numbers, With an Application to the Entscheidungsproblem”)』[1] の中で初めて示された計算不能な機械の証明に関して,簡単な説明を行うことを目的とする(このエッセイでは,チューリングの論文だけでなく,[2] を大いに参考している).
本エッセイで目的とするチューリングの証明は,その後停止性問題として広く知られるようになるものであるが,そこでの多数の道具仕立て,計算機械の構成法や算術化等は,現代的に洗練された解説とは趣が異なっており,今でも一読の価値はあると思われる.
本エッセイは2部構成である.基本的には両方とも独立して読めるように記述している.
第1章では,停止性問題に関して現代的な用語を用いて一般的な解説を行う.ここでの内容は,再帰呼び出しや高階関数等を含むプログラミングの基礎的な知識のみを仮定し,具体的な例示としてはPythonを用いる.
第2章において,チューリングが実際に示した計算不能な機械の証明を行う.内容としては,証明に必要な事項のみに絞ったクラッシュコースではある.計算機械の構成に関しては,基本的にチューリングの論文を追う形で,1つ1つの基礎的な定義を積み重ねて解説を行うため,あまり予備知識は必要としない.しかし,計算機械を数え上げる2.3以降では,集合の簡単な知識(写像,濃度等)が必要である(この辺り知識は[3]を参照).
1.停止性問題とは
停止性問題(Halting Problem)とは,その名の通り,あるプログラムが有限時間内に停止するかどうかに関わる計算理論上の問題である.この問題は,チューリングの計算不能な機械の証明が行われた1930年代当時とは異なり,「”計算”とは何か」ということがコンピュータやプログラミングの普及に伴って,十分に直感的な概念になった現代においては,ごく簡単に理解可能なものである.[ここで述べている”計算”とはアルゴリズムのことであり,”計算可能”とは,ある問題を解決するアルゴリズムが存在することである.逆に,ある問題が計算不能とは,それを解決するアルゴリズムの不在を意味する]
簡単に停止性問題から導かれる結論を述べれば次のようになる:「任意のプログラムが停止する(無限ループしない)ことを判定するようなプログラムは計算可能でない」.[第1章では,チューリングの”機械”とプログラムを同一視する]
1.1.停止性問題の証明
ざっくり証明の道筋を記述すると,しかるに任意のプログラムの停止性を判定するようなプログラムを計算可能と仮定すると矛盾が生じることが示せる.[背理法を忘れている人は少し記憶を辿って思い出してほしい.背理法では,真と思われる命題をあえて偽であると仮定し,推論を進めて矛盾を導くことにより,偽であると仮定した命題が真であることを証明するのであった]
これをプログラミング言語(Python)の形式に従って証明することは容易である.引数を取らない任意のプログラムfについて,次のようなプログラムhaltが構成可能(計算可能)であると仮定すると,矛盾を生じるプログラムGが構成できる.
G = lambda : G() if halt(G) else True
ここで実際にGを実行する場合を考えてみよう.
Gの動作は無限ループするか停止するかのいずれかである.[現実のPythonでは,構文的に無限ループする再帰呼び出しであっても,直ちに最大再帰深度に到達して停止するが,ここでは構文的に無限ループするならば実際に無限ループすると考える.少し言葉を選ぶと,ここでのPythonは可能無限を許容するような計算モデルであると想定する]
まずGは無限ループすると仮定する.するとGは無限ループするのでGの定義におけるhalt(G)はFalseを返し,if文としてはTrueが返ってGは停止する(無限ループしない).Gが無限ループすると仮定して,Gが停止することが示された;これは明らかに矛盾である.同様にして,Gは停止するという仮定から,Gは無限ループすることが示せる.
Gについて考えられる動作のいずれの場合においても矛盾が生じる.そしてこれらはhaltが構成可能であると仮定した結果として導かれた.故に仮定は誤りであり,haltは構成不能(計算不能)である.
1.2.停止性問題の意義
先に簡単に証明を示した停止性問題の意義を端的に述べれば「計算できないこと」の具体例をほぼ初めて示したということになるだろう.
停止性問題は無論,否定的に解決された問題であるが(プログラムが停止するかは一般に判定できない),もしこれが肯定的に解決されていたなら,100万ドルの賞金がかけられている数学上の未解決問題であるリーマン予想でさえ,それを逐次的に検証するプログラムの停止性を評価すれば,瞬く間に解決され得たであろうことを思えば,それの深遠さの一端がわかるだろう.
完全に空想的ではあるが,停止性を評価することにより,ゴールドバッハ予想を証明する例を次に示そう.
def sieve_of_eratosthenes(n):
a, b = [], list(range(2, n + 1))
while b[0] < pow(n, 0.5):
a += b[:1]
b = [k for k in b[1:] if k % b[0] != 0]
return a + b
def sum_of_two_primes(n):
p = sieve_of_eratosthenes(n)
return any([i + j == n for i in p for j in p])
def goldbach_conjecture():
n = 4
while sum_of_two_primes(n):
n += 2
if not halt(goldbach_conjecture):
print('Goldbach Conjecture is TRUE!!')
ゴールドバッハ予想とは,4以上の全ての偶数は2つの素数の和で表すことができると主張する数学上の予想である.
ここでの例ではgoldbach_conjectureにおいて,偶数が2つの素数で表せるかを逐次的に評価し,予想が正しければ際限なく検証を続けるようになっている.これが停止しない(haltの返り値はFalse)ならばゴールドバッハ予想は肯定的に,停止する(haltの返り値はTrue)ならば否定的に解決されるわけであるが,いずれにしても証明はなされる.
1.3.停止性問題の応用
停止性問題には,その他にも重要な応用が存在する:多くの計算不能なプログラムは停止性問題に帰着され得る.1つ例を挙げよう.任意のプログラムに関して”Hello,World!”を出力するかどうか判定するプログラムhwは計算不能である.
なぜならば,hwを計算可能であると仮定すると,hwを用いて次のようなプログラムHALTが構成可能である.
def HALT(f):
def sub():
f()
print('Hello,World!')
return hw(sub)
fが無限に動作するならば,subの定義におけるprintは永遠に実行されないため,hwはFalseを返し,HALTもこれに従う.fが無限に動作しないならば,printは最終的に実行されてhwはTrueを返し,HALTもこれに従う;この動作はhaltを不可分なく実現し,計算可能としている.しかしながら,この結果は,haltが計算不能と証明さている事実と明らかに矛盾する.故に,この結果を導いた仮定は誤りであり,hwは計算不能である.[一般にこのような形で記述される問題,「任意のプログラムが特定の性質を持つかどうか判定するプログラム」は計算不能であることが証明されている.これはライスの定理と呼ばれ,現実のソフトウェアテストの”完全な自動化”が不可能である理論的な根拠となっている]
2.チューリングの停止性問題
第1章では総花的な内容として,停止性問題の簡易的な証明と意義,応用までを述べたが,ここからは本題のチューリングが行った計算不能な機械の証明の説明を行う.[チューリング自身は論文の中で停止性問題という用語は使っていない.Halting Problemという用語は,Martin Davisの著書『Computable and Unsolvability』に由来するらしい([2] からの孫引き)]
『計算可能数とその決定問題への応用』の中で,チューリングは,素朴な対角線論法の適用から興味深い計算機械に関連した集合の性質を示したのちに,そこからの直接の敷衍として計算不能な機械を示している.
ここからの解説は,チューリングの論文の第8章までの流れを追う形で進める.まず手始めに計算機械の定義(2.1)と例(2.2)を示し,計算機械を算術化する記述数(2.3)を解説する.そこから各集合の濃度の関係を整理し(2.4),ごく簡単に万能機械を導入する(2.5).そして最後に計算不能な機械の証明を行う(2.6).
2.1.計算機械の定義
論文のタイトルにもなっている「計算可能数(computable number)」とは,小数表現の各桁を有限の手続き(finite means)によって,機械的に計算する(書き出す)ことができる数を意味している.例えば円周率πは,種々のよく知られた数値積分という有限の手続きによって任意の桁まで書き出すことができ,計算可能数の1つである.一方,仮想的な例ではあるが,無限に並ぶ数のリストを各桁として書き出す他に表現のない数が存在するならば,その手続は無限のリストを含むため,有限的ではなく,計算可能数でない.
計算可能数の性質を具体的(具体的)に調べるため,チューリングは,人が紙とペンを用いて,実際に大きな桁の数の筆算を,限られた手続きに従ってステップ・バイ・ステップに計算するような状況になぞられて計算機械を定義した.
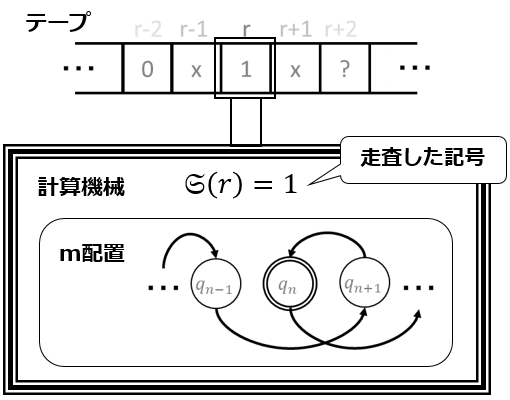
この機械にとっての計算用紙は,何らかの記号を1つずつ書けるマス目で区切られた「テープ」であり,また,計算を行う人(の心的状態)は,機械が取り得る「m配置(m-configuration)」と呼ばれる有限の状態q1,q2,⋯,qrに対応付けられる.次にテープ上のr番目のマス目の記号を走査する(読み取る)ことを考えて,これを記号?(r)と表す.この機械の各時点での可能な動きはm配置qnと走査した記号?(r)により定まり,これの対を「配置(configuration)」と呼ぶ.テープ上のr番号目に紐付いて,記号の走査あるいは印字を行う機構をヘッドと呼ぶ(チューリングは,ヘッドという用語を論文の中で使っていないが,テープレコーダの比喩は十二分に利便なので,本エッセイではこの用語を使う).[ここでの術語は正直わかり難い;後に示される計算機械の具体例と対比すれば,より容易に理解できると思われる.]
チューリングは,バッチ処理的に事前に定めた動作のみを行う機械を「自動機械(automatic machine,またはa機械)」,ユーザと対話的に動作するような,事前にすべての処理が定まらない機械を「選択機械(choice machine,またはc機械)」と呼んで区別していた.今後,計算機械と言った場合には,0か1の記号(第1種の記号)と,その他の記号(第2種の記号)の2種類の記号をテープへ印字するa機械を指すこととする.
計算機械が空白のテープから動作を始めて印字した第1種の記号を,特に機械が計算する列と呼び,その列の前に小数点を付けて2進数と解釈した実数を機械が計算する数と呼ぶ.
動作している計算機械のある時点での完全なスナップショットは,走査したマス番号の履歴とテープ上に印字された記号,m配置によって定まり,これら3つをまとめて「完全配置(complete configuration)」と呼ぶ.[ここでのスナップショットとは,現代における仮想マシンのスナップショットと等価なものである.]
第1種の記号を有限個しか印字をしない計算機械は「循環的(circular)」,無限に印字を行う計算機械は「非循環的(circle-free)」であると言う.[計算機械の動作の有限性に言及することから容易に想像できるように,後の証明において,この非/循環的という性質は重要な役割を果たす.]
特に非循環機械が計算できる列を「計算可能列(computable sequence)」と呼ぶ.また,既に解説をした計算可能数は,計算可能列から得られるものに限定する(ここは簡潔さを優先している;チューリングの定義的にここは厳密ではない).
2.2.計算機械の例
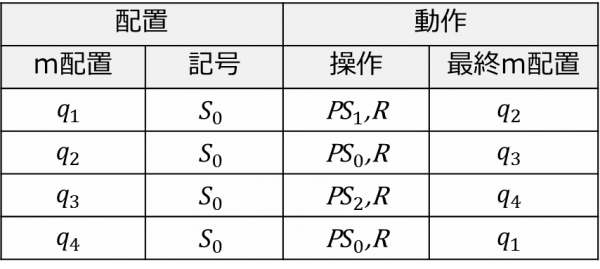
ここから2.1で定義した計算機械の具体例と,その動作を見てみる.次に記述するのは,チューリングの論文の中で最初に登場する計算機械であり,小数表現として1/3を計算する.
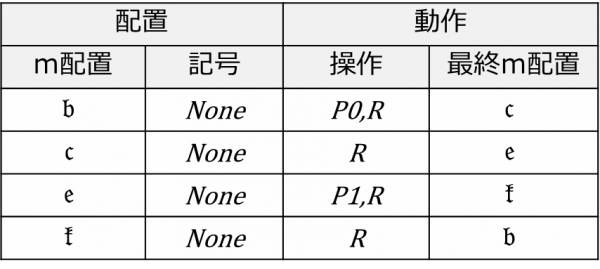
この機械は4つのm配置”?”,”?”,”?”,”?”を持ち,動作として0か1を逐次的にテープ上に印字する.
Noneは走査したマス目が空白であることを表し,P0とP1は各0/1をテープ上の現在のヘッド位置に印字する(一般にPxで記号xを印字する).Rは現在のヘッド位置を右へ1マス移動することを表し,(この計算機械には利用されないが)Lで左への移動を表す.
繰り返される各ステップにおける計算機械の基本動作は,まず,現状のm配置と,ヘッド位置を走査した記号が一致する配置を表から特定し,それに対応する動作における操作を実行,現状のm配置を最終m配置で更新する,という形になる.また,初期のm配置は?と定まっている.
先の機械について,すべてのマスが空白のテープから始動して,m配置が一巡するまで計算を行った場合の各ステップにおける動作(左側)とテープ(右側)の遷移を次に示す.この機械の定義と合わせて順番に確認すれば,大枠としてチューリングの計算機械がどのように動作するのか概ねイメージできるようになると思う.
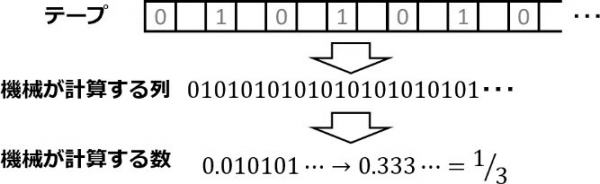
ここではm配置が一巡するまでを示したが,この計算機械はこれら1~14までの動作を無限に繰り返し,最終的に0101010101…の機械が計算する列が得られる;これを機械が計算する数とすれば1/3が得られる.また,この機械は無限に動作し続けるので,定義から非循環的である.
本節では,2進数表現として1/3を計算する機械を例示したが,チューリングの論文では,この後,機械の定義方法として略記やマクロ的な表現などを導入し,より複雑な計算を行う機械が構成可能であることを示す.しかし,これ以上複雑な機械は本エッセイの後の節の説明に必須ではないため,計算機械の例示にこれ以上は深入りしない.
2.3.計算機械の数え上げ
2.1で定義した計算機械は,2.2の例示から容易に想像されるように,適切な配置と動作の表を定義することで無数に得られる.この節では,このような無数に存在し得る計算機械を数え上げることを目標とする.最終的な結果を先取りしてしまうと,構成可能な計算機械の集合ℳは可算集合である.
数え上げの方針としては,任意の計算機械をユニークに自然数へ対応付けることを考える.具体的な手順としては,まず,計算機械の定義を標準形式という分類に落とし込み,それを「標準記述(standard description / S.D)」という限られた文字のみを用いた列へ変換,標準記述に含まれる文字に数字を割り当て,計算機械とユニークに対応づく自然数である「記述数(description number / D.N)」を得る;記述数によってℳから自然数の集合ℕへの単射が得られ,ℳが高々可算集合であることがわかる.
先に記した方針に従い,まず計算機械を標準形式の分類に落とし込む.標準形式においてm配置は番号付けされたq1,⋯,qn(初期m配置はq1と定める)の形で表し,機械が扱う記号も番号付けされたS1,⋯,Sn(特にNone,0,1をそれぞれS0,S1,S2と定める)で表す.この表現を導入することで計算機械を定義する表の各行は次のいずれかに分類,変形できる.
次に(N1)をqiSjSkLqm,(N2)をqiSjSkRqm,(N3)をqiSjSkqmの列として扱うことを考える(Pは必ず行われる動作として省略).任意の機械はこれら列を”;”で繋いで記述できることに注意する.ここでqiをDのあとにi個の”A”が連なった列,Sjを”D”のあとにj個のCが連なった列と考えると,各形式の列は”A”,”C”,”D”,”L”,”R”,”N”,”;”という有限の文字で記述でき,これを標準記述とする.
方針の最後として,”A”を1,”C”を2,”D”を3,”L”を4,”R”を5,”N”を6,”;”を7という数字を割り当てれば,標準記述から直接的に1つの数が得られ,これが記述数になる.
2.2で例示した計算機械を用いて,標準形式と標準記述,記述数の具体例を示す.
まず,各m配置”?”,”?”,”?”,”?”をq1,q2,q3,q4に,None,0,1をS0,S1,S2に置き直す.さらに,ここで右に移動するだけの操作がPS0,Rで書けることに注意すると,2.2の機械は標準形式として次のようになる.
ここから各行でつないだ列を構成し,各記号を所定の文字”A”,”C”,”D”,”L”,”R”,”N”,”;”に置き直すことで標準記述が得られる.
最後に,標準記述の文字を割り当てられた数字に置き直して,次の記述数が得られる.
3133253117311335311173111332253111173111133531
記述数は,その構成法から明らかに任意の計算機械をユニークな自然数に対応付け,数え上げている.このことから,計算機械の集合ℳから自然数の集合ℕへ単射が存在し,ℳが高々可算であることがわかる.また,ℳは無限集合であるから,それは部分集合として可算集合を必ず含み,濃度としてℵ0 ≤ card ℳ ≤ card ℕ = ℵ0,ℳは可算集合である.
2.4.各集合の濃度
2.3では計算機械の集合ℳが可算集合であることを示したが,この節では簡単に,ここまでに定義してきた各事項の集合の関係を整理する.
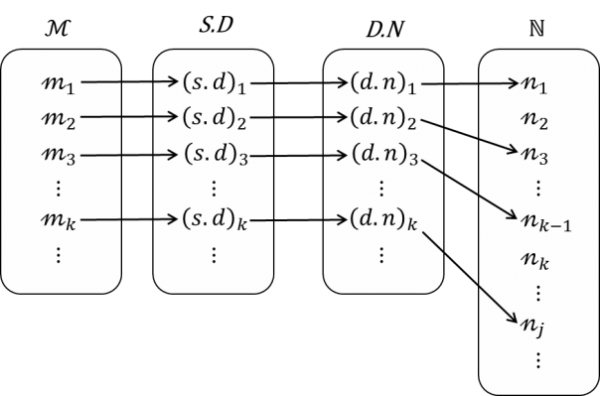
少し繰り返しになるが,2.3では標準記述と記述数を定義した;これらの集合には,構成法から明らかにℳからの全単射が存在し,記述数の集合は自然数の集合へ単射を持つので,最終的に,それぞれの集合は可算になる.次にこれら関係を図示する.
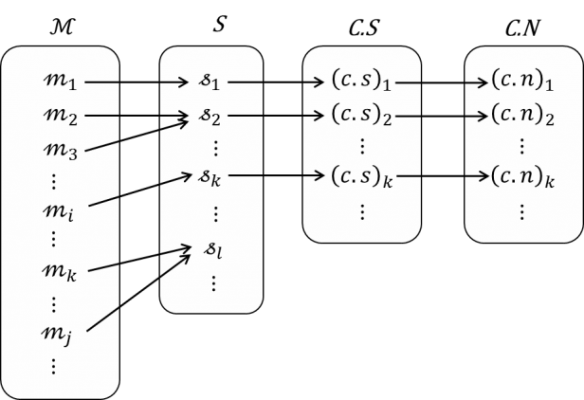
次に,2.1で言及した計算機械の動作に対応する機械が計算する列の集合Sを考える;機械が計算する列は文字通り”機械”から生成されるので,ℳからSへは全射が存在してcard S ≤ card ℳであり,Sは可算である(異なる複数の機械が,同一の列を書き出すことがあることに注意する).また,定義から明らかなように,計算可能列の集合C.Sと計算可能数の集合C.Nは,Sの部分集合と1対1対応を持ち,これらも可算である.次にこれらの関係を図示する.
最終的に,ここまでに定義してきた各事項の集合の濃度は,2.3の結論から派生して,すべて可算であることがわかる.
2.5.万能機械
2.2の例で示した計算機械は,単一の機能のみを持つものであったが,チューリングは論文の中で,ある機械?の標準記述が記載されたテープを受け取り,その機械?の動作を完全に再現する機械?が存在することを構成的に示し,これを「万能計算機械(universal computing machine)」と呼んだ(以下簡潔のため万能機械と呼ぶ).
チューリングの論文の中でも,この万能機械を実際に構成していく部分は,最も独創的で重要な内容の1つではあるが,これの解説を始めると,本エッセイのボリュームが爆増してしまうため,構成に関しては,これ以上深入りはしない.
チューリングの功績として,万能機械によって,物理的に1つの機械を構築すれば,あとはテープ上の記載を変更するだけで多数の機能が実現できる,現代で言えばハードウェアとソフトウェアの可能性を”具体的”に示したことは,しばしば注目されるところである.しかし,論文中において,万能機械は,計算不能な機械の証明で”特に”重要な役割を占めていたことは述べておいて良いだろう;第1章で多用したように,現代のプログラミングにおいて,関数自体を通常のオブジェクトとして扱う高階関数という技法はごく当たり前のものであるが,チューリングが定義した計算機械においては,標準記述と万能機械の導入によって初めて実現され得るものであり,それらの導入は必然的な重要性を持っているのである.[万能機械は,チューリングに先立ち,不完全性定理によって形式的数学の限界の一端を示したゲーデルの仕事の流れから,自己言及性を導入するためのある種必然的な道具であったと言えるかもしれない.ゲーデルが導入したゲーデル数や証明可能性述語は,チューリングの標準記述と万能機械に概ね符合する.]
2.6.計算不能な機械
ここまでの節で道具仕立てが出揃ったので,計算不能な機械の証明に入る.
まず,一見健全な対角線論法に見えるが,実際はそうではない議論を行い,そこでの”見落とし”として計算可能列の集合の興味深い性質を見る.既に検証された命題に対角線論法を適用する;計算可能列の集合C.Sが可算であると仮定する.αnをn番目の計算可能列,?n(m)をαnにおけるm番目の数字とすると,すべての計算可能列は次のようにリストとして列挙できる.
α1 = ?1(1)?1(2)?1(3)?1(4) ⋯
α2 = ?2(1)?2(2)?2(3)?2(4) ⋯
α3 = ?3(1)?3(2)?3(3)?3(4) ⋯
⋯
次にβを,1 − ?n(n)をn番目の数字として持つ計算可能列とする;?n(n)は第1種の記号(0/1)しか取らないため,これは先のリストの対角線上の値をビット反転した列を表している.
β = (1 − ?1(1))(1 − ?2(2))(1 − ?3(3)) ⋯
βは計算可能列なので,先のリストに含まれているはずである.すなわち,あるKが存在して,βは列の各数字が1 − ?n(n) = ?K(n)となるαKである.
β = αK = ?K(1)?K(2)?K(3)?K(4) ⋯
ここで,列の各数字1 − ?n(n) = ?K(n)を,n = Kとして変形すると1 = 2?K(K)となり,1が偶数であるという矛盾した結果が得られる.これはC.Sが可算であるという仮定から導かれた.故に仮定は誤りであり,C.Sは可算でない(!?).
2.4において既に示したように計算可能列の集合は可算である.明らかに何かがおかしい.
直感的には,βはリスト上の各計算可能列に対して,容易に実現可能な減算を適用し,新たな列を生成しているだけであり,一見したところ計算不能な要素はないように思える;しかしながら,ここでの議論の誤りは,やはりβが計算可能であると考えたところにある.
根本的に計算可能列とは,非循環機械が計算できる列であったことを思い出そう.βを構成するためには,計算可能列のリストを列挙する必要があり,それは循環機械と非循環機械を見分けるのと同等の問題を暗に内包している.第1章を読んだ人は既に気がついているだろうが,循環機械と非循環機械を見分けることは停止性問題と同義であり,これは不可能である;先の議論のプロセスは,はじめの段階から見当違いだったのである.
ここでの議論から計算可能列/数の集合について,1つの興味深い性質が見られる:計算可能列/数は可算集合であるにもかかわらず,一般に列挙できない.
チューリングの論文において,この段階では,証明なしに循環機械と非循環機械を見分ける一般的な方法はないことだけを言い,次に正しく対角線論法を用いることで,そのような計算不能な機械を証明できると述べる.
ここからが本エッセイの最後の議論である.
n桁目が数?n(n)であるような,βをより単純にした列β′を書き出す機械を構想する.
β′ = ?1(1)?2(2)?3(3)?4(4) ⋯
まず,任意の機械?の標準記述を受け取り,これを有限回のステップで検証,機械?が循環的ならば”u”,非循環的ならば”s”を書き出す(判定する)ような機械?の存在を仮定する.この機械?と万能機械?を組み合わせることにより,列β′を計算する機械ℋが構成できる.
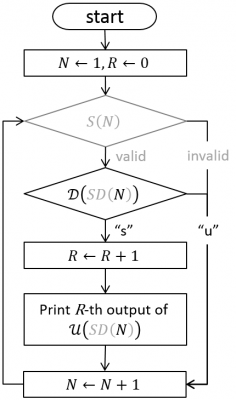
チューリングは論述的に機械ℋの動作を説明したが,幾分か見通しを良くするため,補助的な機械を伴い,各種機械を関数的に表現した場合の動作をフローチャートで次に示す.[ここで,関数への引数の受け渡しや,変数のインクリメント等は,実際にはすべてテープを介して行われることに注意する.]
補助的な機械として,機械SはNが適正な機械の記述数であるかどうかを判定し,機械SDは記述数Nを標準記述に変換する.[これら補助的な機械はチューリングの説明には登場しない.]
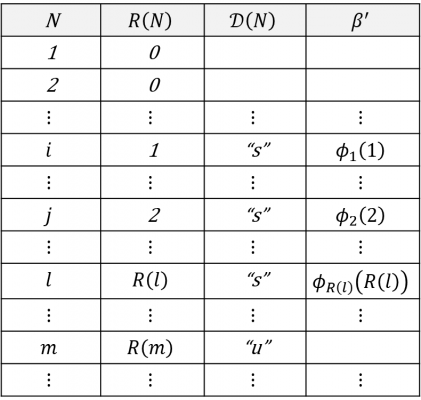
機械ℋは,1から順番に自然数Nを生成し,機械Sの検証を経た後,それを潜在的な記述数として機械?に渡す.その判定結果が”s”であればRを1インクリメント,機械?でSD(N)の動作をR桁まで再現する;そして再現結果の最後の桁のみを,機械ℋのR桁目の出力としてテープへ書き出す.Nに対応するRを特にR(N)として,機械ℋの各変数と動作を次に示す.
機械ℋは構成の方法から非循環的である.また,機械?の仮定と機械?の扱いから各?n(n)の計算は有限回のステップで完了する.仮定より機械ℋは構成可能な機械であるから,対応する記述数が存在するはずである;今これをKとしよう.ここから,1から順番に自然数Nについての各?n(n)を計算していき,機械ℋがKに到達したときに何が起こるか考える.
機械ℋは非循環的であるから,記述数Kにおいて機械?は”u”を返すことはない;しかし,一方,機械?が”s”を返すと考えることも不適切である.このことを,Kにおける機械ℋの動作を追うことで具体的に見てみる.
まず,機械ℋはKを生成し,それについて機械?は”s”を返すと考える.”s”が返されたので,次に機械?がK(機械ℋ)の再現を開始する;少なくともK以前に対応するR桁目までは再現できるはずである.
しかしながら,またKに対応するR桁目まで到達したら,今再現されている機械ℋの中で,再び機械?がK(機械ℋ)の再現を開始する.以下この再現の再現が際限なく行われる.このため機械ℋがKよりも大きい自然数に対応するR桁目を書き出すことはありえない.すなわち,機械ℋは循環的であり,機械?の判定は不適切である.
最終的にどちらの判定もありえないため,この結果を導いた前提は誤りであり,機械?は存在せず,計算不能である.
3.終わりに
このエッセイでは,前半において多少広がりのある停止性問題の全般的な解説を行い,後半でチューリングの論文を追いながら,最終的に計算不能な機械の証明を行った.
焦点を絞り,出来る限りわかりやすい説明を試みたつもりだが,著者の明らかな力量不足から理解に苦しむ点も全体を通して散在しているところと思う.そのような点にぶつかった読者には,大変申し訳ないと思う.
最後なので少し個人的な話をしよう.私がチューリング機械や停止性問題という言葉を初めて聞いてから既に十数年が経過しているかと思うが,実際に,それらがどのようなものであるのかということを具体的に知るようになったのは,ここ数年であった.
計算モデルや計算可能性の限界という何とも興味をそそられる題材に長く憧れは抱いていたが,計算理論という,なにやら難しそうな言葉に恐れをなして必要以上に近づこうとはしていなかった.
これが変わったのは参考文献[4]との出会いであった.計算理論がプログラミング言語の直接的な延長線上で議論され得ることは,自分にとってはとても新鮮であった.[後知恵ではあるが,チューリング機械やラムダ計算でなく,実在のプログラミング言語や,現実的な擬似言語を計算の定義として導入している書籍は多数存在しているようである.] ここでの観点は,第1章において幾分か取り入れられている.願わくは,本エッセイによって,自分が感じたのと類似の新鮮さが多少でも読者に伝わっていればと思う.
第2章を読んでチューリングの実際の仕事に興味が湧いた読者は,ぜひ参考文献[2]を読んでもらいたい.時間はかかると思うが,素晴らしいガイドと共に,このエッセイでは伝えきれなかったチューリングの独創性を何十倍も感じてもらえることと思う.
4.参考文献
- Turing, A. M. (1936). On Computable Numbers, With an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, 42. 230-265.[↑]
- チャールズ・ペゾルド (著), 井田哲雄, 鈴木大郎, 奥居哲, 浜名誠,山田俊行 (訳).(2012). チューリングを読む — コンピュータサイエンスの金字塔を楽しもう.日経 BP 社.[↑]
- 松坂和夫. (1968). 集合・位相入門. 岩波書店.[↑]
- 鹿島亮. (2008). C 言語による計算の理論. サイエンス社.[↑]