Knuth: The Art of Computer Programming の話
2022年12月05日 月曜日

【IIJ 2022 TECHアドベントカレンダー 12/5(月)の記事です】
クリスマスといえば, 英国王立研究所が1825年から続けている「クリスマス講演」が有名で, 岩波文庫にあるFaradayの「ロウソクの科学」はその1860年の講演だ. それに比べればまだ20年くらいだが, スタンフォード大学のKnuth教授も毎年「クリスマス講義」を続けている. しかし今回のブログはそのKnuthによる大著, The Art of Computer Programming(以後TAOCP)が話題である.
上段の左の横積みは, 英語版TAOCPの, 上から第1, 2, 3, 4A巻の背表紙(うすよごれているが, 私の所持品). 右はこの10月に送られて来た第4B巻の表紙. 下段は日本語版TAOCP第1, 2, 3, 4A巻の表紙(アスキードワンゴ刊).
最近の若い皆さんは, The Art of Computer Programmingにほとんど興味がないというか, そもそもその存在も知らないのではと思う. TAOCPは, スタンフォード大学のDonald E. Knuth教授がライフワークとして書いているアルゴリズム解説書のシリーズである. 第1巻初版の刊行は1968年で, 著者は30歳.
それから50年以上過ぎたが, まだ刊行は続いている.
その本の前書きによると, 全体で7巻, 12章の計画であった. 現在第4巻, 第7章の途中まで来た.
その頃の本は, 活字を組み合わせてページを構成するので, 数式の多い本は, 著者の思う通りに作るのが大変であった. そこでKnuthは, 本の執筆を中断し, 組版システムの開発に取り掛かる. これが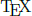 である. さらに活字の形も気に入らなくて, フォント作成システム
である. さらに活字の形も気に入らなくて, フォント作成システム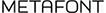 も開発した.
も開発した.
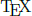 と
と を手に入れたKnuthは, それを使い, 第1, 2, 3巻を改訂, 1997, 98年に刊行した.
を手に入れたKnuthは, それを使い, 第1, 2, 3巻を改訂, 1997, 98年に刊行した.
私は 以前の第1巻を見て, 特にマシン語MIXの扱いについて, これは奇妙な本だと思い, その少し後に出た和訳にも関心はなかった.
以前の第1巻を見て, 特にマシン語MIXの扱いについて, これは奇妙な本だと思い, その少し後に出た和訳にも関心はなかった.  版の1,2,3巻は商売がら購入し, 時折眺めては, こんなことまで(例えばフーリエ変換を使う乗算)書いてあるかと驚いた.
版の1,2,3巻は商売がら購入し, 時折眺めては, こんなことまで(例えばフーリエ変換を使う乗算)書いてあるかと驚いた.
記憶が定かでないが, 1995年から2000年頃, アスキーから, TAOCPを改めて和訳出版したい, ついては監訳を頼みたいといわれた. 私も大学を離れ, 多少時間も出来たのでやってみることにした. そして若手の諸君による3巻までの和訳が, 2004年~2006年に出版された.
第4巻については, 以前から, 原稿は出来ているらしい, そろそろ出るかもと噂されていたが, 中々現れないうちに, 英語では分冊形式で, 第4巻分冊2, 分冊3というふうに2005年から出版され始めた. そこでアスキーは, その分冊も, 1,2,3巻同様に和訳刊行を始めた. その辺りまでは, 私は監訳者だったが, 2008年から分冊0, 分冊1が出ると, 興味のある話題だったので, 私が自分で翻訳した.
やがて, 英語版は, 分冊0,1,2,3,4を合わせ, 第4A巻として2011年に刊行され, 日本では, 出版社がアスキーからアスキードワンゴに変り, そこから分冊の和訳を集めて, 第4A巻の和訳が出た.
第4B巻は, その後出版されるはずの, 分冊5,6,7,8,9を併せて作られる予定で, まず分冊6(2015年)と5(2019年)が出た. 分冊8と9については, ベータテスト版がネット上にはあるが, 紙の分冊の出る様子はない. すると突然今年の6月ころ, 分冊5と6とだけで第4B巻にするという話になった. その第4B巻は10月に刊行された. 第4B巻のカバーの裏表紙には, Knuthの依頼で私が書いた紹介文が印刷されている.
このシリーズについて, Bill Gatesが“If you think you’re a really good programmer, read Art of Computer Programming” といったとか, エラーの発見に対して贈られる小切手風の謝礼について, “among computerdom’s most prized trophies” といわれたりする(Wikipedia)が, それほどのものではない. どちらかといえば, 私はTAOCPを読むのは奨めない. その理由について追い追い述べることにする. まず本書を理解するには忍耐がいる. 推察力がいる. ひょっとしてこうかもしれないという機転力がいる. また例えば第2巻にソートの各種の方法が詳述されているが, 今や自分でソートのプログラムを書く人はいるまい. foo.sort()(Python)や(sort foo <)(Scheme)のように出来るからだ. もっとも, クイックソートやヒープソートの原理が分ると感動するが.
この本の問題点は山のようにあるが, その第一はアルゴリズムが自然言語(英語)で記述してあることだ.
それについてKnuthは, 「高級言語を使うとしたら何を使うべきか. 1960年代ならば, たぶんAlgol Wを選んだ. 1970年代になったらPascalで書き直さなければならなかった. 1980年代ではきっとCに変更していた. 1990年代には, C++に切り替え, もしかするとさらにJavaに変えていたかもしれない. 2000年代にはさらに別の言語が正当な言語になっていることは間違いない. 言語の流行り廃りに合わせて本を書き直す時間はない.」という. (第1巻分冊1序文)
実際はCを基本とし, C++へ多少拡張したCWEB(https://web.archive.org/web/20211020184416/http://tex.loria.fr/litte/wc.pdf)を使っているらしく, 本に書く時, 英語に変えている. アルゴリズムの入れ子の関係は, 句読点や接続詞を使って示すが分り難い. せめてかっこくらいは使って欲しいところだ.
第二に, 低レベルで記述するので, アルゴリズムの本質が見通せない.
TAOCPの話となれば, アルゴリズム記述の例を書かなければならない.
例えば, 単純交換(Plain change)による4要素の順列(横に読む)
0123 0132 0312 3012 3021 0321 0231 0213 2013 2031 2301 3201
3210 2310 2130 2103 1203 1230 1320 3120 3102 1302 1032 1023
は, 0123の右の2個を交換すると0132になり, その中央の2個を交換すると0312になり, その左の2個を交換すろと3012になり…というように, どこかの隣同士を交換して, 24個の全順列を生成したものである.
この構造は, 最初の4個を上から下に書き. その次の4個をその右に下から上に書き, その次の4個をその右に上から下に書き, …としてみる. すると左の列最上段は, 012の右端に3を置き, 下へ進みながら3の位置を次々と左へずらしたものであり, 次の列の最下段は021に左端に3を置き, 上へ進みながら3の位置を次々と右へずらしたものである.(下の表の左半分)
0123 0213 2013 2103 1203 1023 0000 0010 0020 0120 0110 0100
0132 0231 2031 2130 1230 1032 0001 0011 0021 0121 0111 0101
0312 0321 2301 2310 1320 1302 0002 0012 0022 0122 0112 0102
3012 3021 3201 3210 3120 3102 0003 0013 0023 0123 0113 0103
上の表の右半分は, 左の順列のそれぞれの逆転表である. 順列a0a1 . . . an−1の逆転とは, i番目の位置に, 要素aiの右にあるaiより小さい要素の個数を書く. 例えば, 左下3012の逆転は, 0, 1, 2の右にはそれより小さいものはないので左の3個は000; 3の右は3個とも小さいので, 右端が3になる. 逆転表の左の列の右端(3に対応)が, 0123と進むが, 順列012に3を右端から数えて0番目, 1番目, 2番目, …の位置に挿入するのと合っていることに気付く.
また, この逆転表は, よく見ると, 混合進法のGray Codeになっている. そういう訳で, この順列生成アルゴリズム7212Pは, Gray Code風に逆転を順に作り. そのcjから交換位置を知り, 次の順列を作る. 配列ojは, 桁jが増えつつあるか, 減りつつあるかを記憶する. 以下でnは順列の要素数.
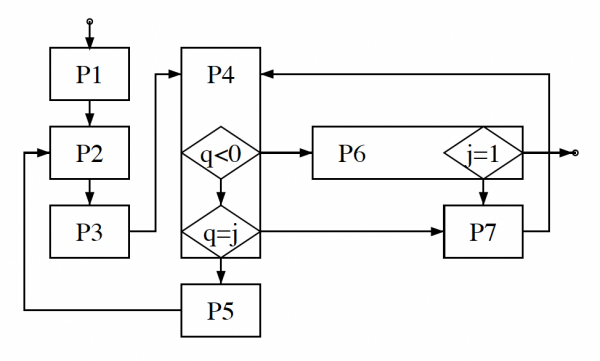
P1. [初期設定] 1 ≤ j ≤ nについて, cj ← 0, oj ← 1 とする.
P2. [訪問] 順列a1a2 . . . anをたどる(印字する, 使用する.)
P3. [変更の準備] j ← n, s ← 0とする.
P4. [変更の準備が出来ているか?] q ← cj + ojとする. q = jならP7へ進む. q < 0ならP6へ進む.
P5. [変更] aj−cj+s ↔ aj−q+sを行う. cj ← q として, P2に戻る.
P6. [sを増加] j = 1なら終了する. そうでないなら, s ← s + 1とする.
P7. [方向を切り替える] oj ← −oj , j ← j − 1とする. P4に戻る.
TAOCPのアルゴリズムは, このようにP1, P2のようなステップで出来ていて, 各ステップで変数を設定
したり, 判定して別のステップへ進んだりし, 最後にどこへ進むともいわれなければ, 次のステップへ進
むという仕掛けで, これもアルゴリズムの見通しを困難にする.
この方式は, 世の中でプログラムを書き始めたころに流行した, 流れ図(フローチャート)を使ってのプログラムの考え方で, TAOCPは, 初版が早く出版されたせいもあり, 旧態然とした方式から離脱できないでいるのである. 頑に昔の方式を踏襲すると, 進化の速い計算機の世界では, 異様な感じになるのは止むを得ない.
TAOCPのアルゴリズムで気に入らないのは, 配列の番号が1から始まることである. 次に示すのは, 0から始まるようにして, 私がPythonで書いたものだ. Pythonにはgoto文がないので, そこは関数呼出しで代用する. 最後に呼出しから連続して脱出するが我慢する. 関数p1, p2などがステップP1, ステップP2などに対応する. (本家のCWEBにもgotoはなく, 関数を呼ぶから, そのままのアルゴリズムを示してくれた方がよかったかも.)
000 def plainchange(n):
001 """Algorithm TAOCP 7212P"""
002 a = [x for x in range(n)] #順列aの初期化[0, 1, 2, 3]
003 def p1():
004 global c, o
005 c = [0 for x in range(n)] #cの初期化[0, 0, 0, 0]
006 o = [1 for x in range(n)] #oの初期化[1, 1, 1, 1]
007 p2()
008 def p2():
009 print(a); p3() #aを印字
010 def p3():
011 global j, s
012 j = n – 1; s = 0; p4()
013 def p4():
014 global q
015 q = c[j] + o[j]
016 if q < 0: p7() #c[j]が下限に来た
017 elif q > j: p6() #c[j]が上限に来た
018 else: p5()
019 def p5():
020 l = j – c[j] + s; m = j – q + s
021 a[l], a[m] = a[m], a[l] #a[j – c[j] + s]とa[j – q + s]を交換
022 c[j] = q; p2()
023 def p6():
024 global s
025 if j > 0: s = s + 1; p7() #j = 0なら終了
026 def p7():
027 global j
028 o[j] = -o[j]; j = j – 1; p4() #o[j]を反転する
029 p1()
030 plainchange(4)
TAOCPの不思議は, 再帰呼出しを使わないことである. (第8章の題名がRecursionなのでそれまでとってあるのか.) 補助変数を用意し, 再帰と同じことを自分で管理する. 本書の初版が出たころは, 再帰呼出しの出来るプログラム言語はなかったからかも知れない. またTAOCPは機械語命令の総実行数でアルゴリズムの優劣を評価しようとしたためだろうか.
上の解法は, 4要素の単純交換の順列は3要素の単純交換の順列から作るという方式なので, 当然再帰で書きたくなる. 次は私がそういう発想で書いたものである. (Pythonによる.)
3が左へ行ったり右へ行ったりする元の列, 012, 021, 201, 210, 120, 102は, 01に対して2を左へずらし, 10に対して2を右へずらして作る. 最後は0に対して1を左にずらす.
000 def plainchange(n):
001 """Algorithm TAOCP 7212P"""
002 def mix(ps0, m, t):
003 def mx(i, d): #mをps0のi番目に挿入
004 ps1 = ps0[0:i] + [m] + ps0[i:len(ps0)]
005 if m == n – 1: print (ps1, end = ' ') #ps1を印字
006 else: mix (ps1, m + 1, d)
007 if t:
008 d = True
009 for i in range (m + 1): #mを右から左へ挿入
010 mx (m – i, d); d = not d
011 else:
012 d = m % 2 == 1
013 for i in range (m + 1): #mを左から右へ挿入
014 mx (i, d); d = not d
015 mix ([], 0, True)
016 plainchange (4)
004行目のps0[0:i] + [m] + ps0[i:len(ps0)] はps0の左からi番目にmを挿入する. 007行目からの関数mix(ps0, m, t)は, tが真なら, mをps0の右から左へ順に挿入し(上の表の上から下), 偽なら左から右に挿入する(下から上).
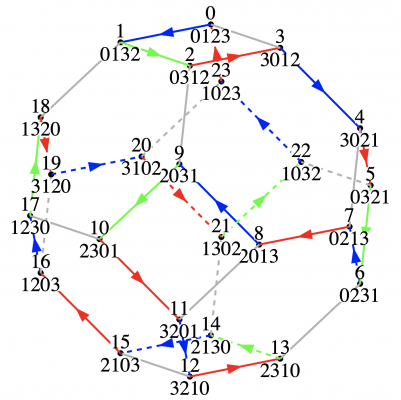
余談だが, n = 4の単純交換による順列は, 上の図のように, 切頭八面体(truncated octahedron, 正八面体の6個の頂点を, 8個の正三角形が正六角形になるように切る. 切口は正方形)の24個の頂点に対応する. 単純交換の表で, 3が左から右, 右から左に移動するのは, それぞれの正方形の辺上での移動に対応する. 隣の列は隣の正方形になる. この図の赤, 緑, 青は, どの位置で交換があったかを示す. 青緑赤青, 赤緑青赤を繰返し. 順列全体の生成は, すべての頂点を通るHamiltonian Pathになっている. 切頭八面体は私の好きなArchimedean多面体である. 立体の中心を原点とする各頂点の座標は{0,±1,±2}だけで構成される.
また余談だが, 単純交換はhttps://www.youtube.com/watch?v=pvFaHdkmx44にあるように, 教会の複数の釣鐘の鳴らし方の順番として考案された. 釣鐘の振動に慣性があるので, 遠方のと順番を交換が急には出来ないという事情による.
想像されるように, TAOCPの原稿は勿論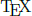 で書いてある. 翻訳権を取った出版社には, その原稿が屆くので, 翻訳はその
で書いてある. 翻訳権を取った出版社には, その原稿が屆くので, 翻訳はその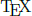 ファイルの数式や表はコピペし, 地の文を英語から日本語にする. 図は別のファイルにあるらしく, そこへの参照番号になっている.
ファイルの数式や表はコピペし, 地の文を英語から日本語にする. 図は別のファイルにあるらしく, そこへの参照番号になっている.
なにしろ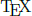 開発者による
開発者による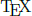 文書だから, なかなか面白い. 参考になるのは少しでも似たパターンがあると, すぐにマクロコマンドを定義して使うところである. 例えば,
文書だから, なかなか面白い. 参考になるのは少しでも似たパターンがあると, すぐにマクロコマンドを定義して使うところである. 例えば,
‘1 s1 s3’, ‘1 s2 s4’, ‘1 s3 s5’, ‘1 s4 s6’, ‘2 s1 s4’, ‘2 s2 s5’, ‘2 s3 s6’, ‘3 s1 s5’, ‘3 s2 s6’.
と出力したい時は
$$\def\\#1#2#3{\hbox{‘$#1\,s_#2\,s_#3$’}}
\\113, \\124, \\135, \\146, \\214, \\225, \\236, \\315, \\326.$$
と書く. 上の出力部分の原稿はもちろんこのマクロで書いてある.
ちなみにこれはn=3のLangford対で, 1,1,2,2,3,3を, 1と1の間には他の数字1個, 2と2の間には他の数字2個, 3と3の間には他の数字3個を置く可能性を示すもので, ‘3 s1 s5’は3を1番目と5番目に置くという意味である. 1,2,3とs1, s2, . . . , s6を1回ずつ含むように可能性を選ぶと解になり, 解は2通りある.
本書の特徴のもうひとつは, 演習問題の数の膨大なことだ. 分冊5のDancing Linksの章は450番まで, 分冊6のStisfiabilityは526番まであり, 気が遠くなる. それもそれぞれが相当難しい. もちろん詳細な解答もあるが, 解答を読んでもすぐには分らないことが多い.
全体として, 内容を理解するには, プログラムを書き, 実行してみなければならない. もっともそうやって, 私はエラーも沢山見付けた.
TAOCPには, 本書で何らかのエラーを最初に見付けた人には, $2.56を贈ると書いてあり, 小切手風の謝礼が送られてくる. 以前は$2.56の実際にある米国の銀行の小切手で, 換金出来たが, その小切手の写真をネットに掲載する人が増え, 2008年頃にトラブルになった.
今はSan Serriffeという架空の銀行の, ダミーの小切手が使われていて, 記念品に過ぎないが, 希望すれば米ドルが屆くらしい.
(San Serriffeはフォントの一種サンセリフ(Sans Serif)をもじった架空の国名で, インド洋を少しずつ東へ移動し, セミコロンの形をしているなど印刷用語だらけの島国である.)
ではメイルでエラーを報告するとどうなるだろうか. 私の経験では, メイルを送って半年くらいするとスタンフォード大学から郵便が来る. 中はこちらから送ったメイルのハードコピーで, 印刷上のエラーだとその横に$1.00と記入してある. 少し複雑なエラーの記述には, Knuthが克明に読んだ形跡があり, 鉛筆でのゴチャゴチャなコメントと, $1.00が書いてある. 問題はその文字が読めないような悪筆で, また送って半年も経っているから, もう何が疑問だったかも忘れていて, 読む気にならず申し訳けなく思っている. そして小切手風の謝礼が同封されている.
この本でKnuthの徹底振りが分るのは, 索引の人名に, Wada, Eiiti (和田英一)のように, 出身国の文字でも併記されていることだ. 日本の漢字と中国の漢字が厳格に区別されていることにも驚く. Knuthは, 中国人ではないのに, 中国の漢字で, 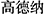 とあるから笑ってしまう. (「高」の上の点は, 日本のは立っていて, 中国のは傾いている. 「納」の糸偏の点は, 日本は3点あり, 中国は一画)
とあるから笑ってしまう. (「高」の上の点は, 日本のは立っていて, 中国のは傾いている. 「納」の糸偏の点は, 日本は3点あり, 中国は一画)
以上長くなったが, 要するにTAOCPはこのような本である. すごい本だが始めにも書いたようにこの本を読むのを私は奨めない. 現在では基本的アルゴリズムより, ヒューマンインターフェースやネットワークなど, Knuthが計画した頃にはなかった領域が重要になっている. そちらをマスターしてから余力と関心があれば, TAOCPにも取り組んで欲しい.
Knuthの小切手風謝礼. 左はWikipediaの写真. 上から順に番号と日付; 受取人名と右に十六進法の金額0x$1.00; One and ∼∼∼∼ no/256 HEXADECIMAL DOLLARS のように普通の小切手風にある(日常使う小切手では十進法で書く). 右は私に送られて来たもの.
上の写真は, 2008年夏, カリフォルニア州のComputer History Museumに行く用事があった折, スタンフォード大学近くのKnuthの家を訪れ, Knuthと歓談した時のもの. 夫人のJillがシャッターを押した.
Knuthの家には, 小型のパイプオルガンがあることも知られている.
https://www-cs-faculty.stanford.edu/~knuth/organ.html
Knuthの本には, エラーを見付た時は,
taocp@cs.stanford.edu
に知らせるように書いてあるが, Knuth自身は1990年に電子メイルを止めたと公言している. TAOCPの執筆の時間を確保するためという. しかし, TAOCPについて連絡が必要な時は, 秘書の名前を送信者としてメイルが屆くことがある. 自分のメイルアドレスはないらしい.

Twitterフォロー&条件付きツイートで、「IoT米」と「バリーくんストラップ」と「バリーくんシール」のセットを抽選でプレゼント!
応募期間は2022/12/01~2022/12/31まで。詳細はこちらをご覧ください。
今すぐツイートするならこちら→![]() フォローもお忘れなく!
フォローもお忘れなく!