『人月の神話』新人エンジニアにオススメする技術書
2020年07月02日 木曜日

CONTENTS
はじめに
こんにちは。高井です。私は現在IIJでBtoBサービスのネットワークシステム開発に携わっています。運用やサポートではなくシステム開発部門です。IIJに入社する前からもWebアプリケーションやWebサイト開発業務に携わってきました。そんな私は予てより数学や哲学的なことを考えるのが好きでした。そのためシステム開発をする際には技術的な知識だけでなく、物事の抽象化やモデル化について考えることがあります。
今回のブログの企画は「新人エンジニアにオススメする技術書」ということらしいですが、特定の本を紹介するだけでは読む方もなかなか興味が持てないのではないかと思い、ちょっとしたストーリー性のある記事のなかで書籍を紹介できないかと考えながら筆を執ることにしました。新人エンジニアに知っておいてもらいたい概念として「モデル化」について話をしていきます。少々長いですがお付き合いください。全てを読むのに20分ほどかかるので途中で飽きたらまとめへ飛んでください。
世界の真理を知る
地球に住んでいる我々は、一日の空を見て何を思うだろう。太陽が動いている。星が動いている。
「地球を中心に、周りを天体が動いている」——これは天動説と呼ばれるモデルである。
そのように感じるのは自然かもしれない。
しかし我々は、天動説というモデルは誤りであることを知っている(注1)。
(注1)科学の世界では絶対的に正しいことなど存在しない。我々がモデルとして最も適切であると合意しているに過ぎない。より真理に近い新たなモデルが登場する可能性は常にある。
いつの時代も人は世界をモデル化して解釈している。
「モデル(Model)」という言葉は「ファッションモデル」や「モデルとなった作品」のように使われたりもするが、ここでいうモデルは「経済モデル」や「原子モデル」のような「事象の構造を抽象して論理的に形式化したもの」(三省堂 大辞林 第三版より抜粋)の意味するものを指している。
普段でも我々は身近なことをモデル化して解釈している。私の話をしよう。私は会社に行かなければならない。会社は朝9時から始まる。会社は夜6時に終わる。家に帰ったらプライベートなことをする。そして就寝する。
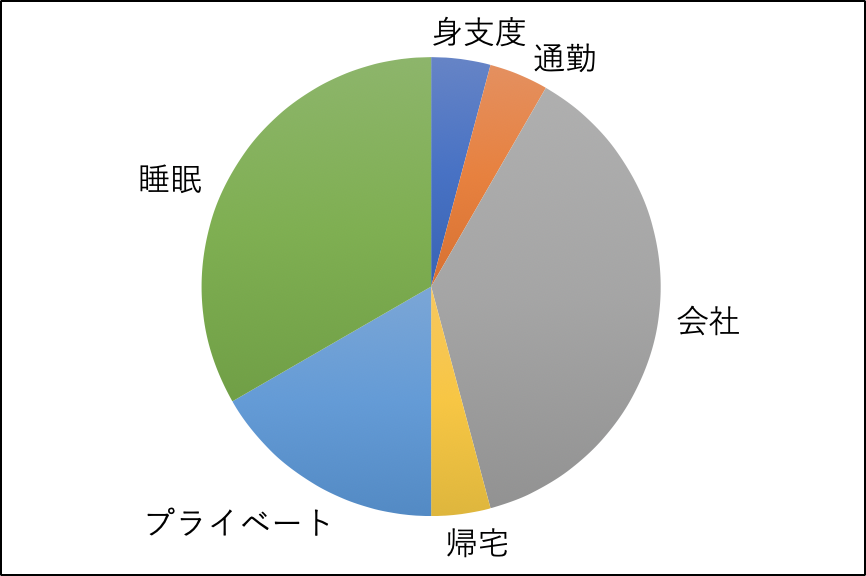
ここに図を貼ってみた(注2)。この図では次のことを説明している。私は朝起きて1時間で身支度をして1時間で通勤をする。会社には休憩時間を含めて9時間いる。帰宅には1時間かかり、帰宅後はプライベートの時間を過ごす。睡眠時間を8時間とするとプライベートな時間は4時間のようだ。1時間、1時間、9時間、1時間、4時間、8時間。これで24時間である。
(注2)この図はいま私が作成したものだがCC0ライセンスとしよう。ライセンスにはクリエイティブ・コモンズや MIT, GPL といったものある。興味があればこれらが何を意味するのか調べてみるとよいだろう。
我々は普段何気なくこのような「モデル」を思い浮かべながら、友達から飲み会に誘われたら予定があるかどうかを判断したり、休日には何をするかを考えている。
このモデルを突き詰めれば「私」が社会人になってから人生を全うするまでの限られた時間に、何にどれだけの時間を捧げることができるかを知ることができるだろう。おっと、それを想像として悲観する必要はない。そんな単純なモデルで表現できるほど人生は単純ではない。人生には心を震わせて感動するような出来事がいくつもある。
芸術的な作品や感動的な音楽との出会い。身近な人の結婚。子供の誕生。久しぶりに会う旧友や家族との団欒のひととき。はたまた、Amazon Prime Videoで『Silicon Valley(シリコンバレー)』といった海外ドラマを鑑賞した日。ニコニコ動画やTwitchでゲーム配信を観ながら世界中の誰かとコミュニケーションする時間。2ちゃんねる用語のようなインターネット特有の文化やミームを楽しむこともある。いまここに書き並べたのは、この記事の執筆期限に追われながら休日の朝に思いついたキーワードを書き殴っただけであり、こういうときに例示するキーワードとしては相応しくないかもしれない。しかし今の私には例文を考える時間がないのだ。ともかく、人生は想像以上に素晴らしいのである。このような単調なモデル化で人生を語ってはならない。話を戻そう。
モデル化という行為は誰もが無意識に行うことでもある。一方で、取り扱うのが難しい対象に対しては誰かが意識的にどのように抽象化できるかを考えてモデルを提唱する。そうして登場するのが「天動説」であったりするのである。
人月の神話
『人月の神話』という本を聞いたことがあるだろうか。
『人月の神話』(にんげつのしんわ、英: The Mythical Man-Month: Essays on Software Engineering)は、フレデリック・ブルックスが著したソフトウェア工学とソフトウェアプロジェクト管理の書籍である。
人月の神話という本についてはこの記事を執筆している時点で Wikipedia に上記のように書かれている。なかなか的確な文章であるので引用させていただいた。
ところで、先にも述べたように、残念ながら今の私にはこの記事を執筆する時間がない。少々強引ではあるが、インターネット上に公開されている文書やブログ記事を引用しながら話を進めたい。ただし、Wikipedia のような誰でも編集できるコンテンツは信憑性や表現に問題があるかもしれない。参考情報として読む分にはよいが Wikipedia の記述を情報の根拠として扱うことは望ましくないことを付け加えておこう。
さて、『人月の神話』という本の表紙にはタールの沼と複数の獣たちの絵が描かれている。そして、4ページ目に次のような記述がある(注3)。
太古の昔から、タールの沼に落ちた巨大な獣が死のもの狂いで岸に這い上がろうとしている光景ほど鮮烈なものはない。恐竜やマンモス、それにサーベルタイガーがタールに捕えられまいとしてもがく様が目に浮かぶ。激しくもがけばもがくほどタールは一層絡みつき、どんなに力強い獣でも、また賢く器用な獣でも、ついには沈んでいってしまう。
大規模システムプログラム開発は、過去10年以上もの間そうしたタールの沼のようなものだった。そして多くの強大な獣たちがその中で激しくのたうちまわってきた。たいていは稼働システムを作り、這い上がってきたものの、ゴールとスケジュール、それに予算にかなったものはほとんどなかった。
規模の大小、また大量動員あるいは少数精鋭であろうとも、開発チームは次から次へタールでがんじがらめになってしまう。問題を引き起こす原因は1つだけではないように思われる。原因が1つだけなら、足のどれか1本くらいはタールから抜けるはずだ。だが、同時かつ相互に影響し合う要因が重なり合っているので、動きがどんどん遅くならざるを得ない。この問題が執拗でやっかいなことはだれにとっても驚異であり、その本質を理解するのは困難である。しかし、問題を解決しようというならば、理解するように努めなくてはならない。
― 『人月の神話』 フレデリック・P・ブルックス,Jr.、滝沢徹、牧野祐子、富澤昇、2002年、p.4
(注3)「だれにとっても驚異であり」の部分は原文ママである。「驚異」というより「脅威」であるように思う。
この本はシステム開発や案件のプロジェクト進行を行う現場において、システムを完成させ納品しなければならない期日までに開発が間に合わない状況に陥ってしまう問題、何週間も残業したり徹夜してもプロジェクトの終わりが見えない状況(そのような状況は「デスマーチ」と呼ばれる)を取り上げて、なぜそのような状況が起こってしまうのか、作業見積もりの一つの基準である「人月」あるいは「工数」というものがどういう性質のパラメータであったのかについて読者に問いかける、そのような内容の本である。
この記事を読んでいる人の中に「人月」という言葉を聞いたことがない人がいるかもしれない。簡単にこの言葉の意味を説明しておこう。この言葉は、主にシステム開発をする際に必要な作業時間を表すものであり、この作業時間自体は「工数(こうすう)」と呼ばれる。ある仕事を完了させるのに工数がどれだけ必要なのか、業務をする上で私はこの質問をしばしば浴びせられる。「3ヶ月後にシステムをリリースする計画があるが、それに合わせてとある機能開発を行いたい。その開発にどれだけ工数がかかるか教えてほしい」といった具合である。
「開発経験がないからまずは5日間ほど技術調査をして、それから設計をして――。実装して動作テストしてその修正まで完了するのには6週間もあればできそうか」と私は考えを巡らせる。週休2日制(注4)であれば1週間における稼働日は5日間。そして1ヶ月を4週間とみなせば6週間は1.5ヶ月である。このようなとき「技術調査には5人日(にんにち)かかり、この開発全体では1.5人月かかる」というように表現する。これが「人月」というものである。
(注4)正確には完全週休2日制である。社会人になったのであれば、就業規則や労働に関する法律にも関心を持ってみるとよいだろう。
さて、この本のポイントを説明するためにひとつのブログ記事を紹介したい。この本についてよくまとめられている。
第0回の記事には次のように書かれている。
そもそも、タイトルの「人月の神話」とは、「人(労働人数)と月(投下時間)が交換可能である」という、ソフトウェア開発の世界では「常識」とも言うべき考え方が、「単なる神話に過ぎない」と述べているわけです。これは、凄いことです。しかし、それから40年が経過した今も、人と月は交換可能であるかのように扱われ続けており、そして、非常に悲しいことに「デスマーチ」なプロジェクトが量産されています。
まとめの記事には次のように書かれている。
人月の神話とは?
人月の神話というのは、ソフトウェア開発の”単位”である「人月」という概念が、神話に過ぎない(つまり、意味をなさない)という悲しい真実を軸に、ソフトウェア開発が如何に困難を伴うものであるかを説いた名著です。一言でいえば、10人月の仕事=1人で10か月かかる仕事は、「人月という単位が絶対であれば”10人で1ヶ月”でできるハズ」だが、そんなことは起こりえない、というお話です。そして、この状況を打破し、遅延したプロジェクトに100人投入して一瞬でシステムを完成させるような「魔法の道具(=狼男に決定打を与える”銀の弾”)」は存在しない*と結論付けられます。
先の例であれば、私が1.5人月かかると見積もりをした機能開発について、「1人で担当すれば1.5ヶ月(6週間)かかるだろうが、3人で共同開発すれば2週間で終わるだろう」という話である。「労働人数」と「投下時間」が交換可能であるのかという話であり、実際、私はWebシステム開発をする現場でそのような「交換」がしばしば行われるのを目にしてきた。そしてそれが計算通り3人の力によって2週間で終わることもあれば、3人がかりで1.5ヶ月が過ぎてもシステムがリリースできる状態にならないこともあった。
これはどういうことなのか。少し紐解くと、前者はもともと1人でやっても2, 3週間で終わるような比較的簡単な内容であったということだ。一方、後者はシステムの完成に必要な要件定義が曖昧で、開発中に仕様が変更されるようなことも起き、開発を計画通り進めることができなかったのである。見積もりにはそうした側面もある。先ほど私が1.5人月と見積もった機能開発では、何を根拠に1.5人月(6週間相当)であると判断できたのだろうか。
ここで比喩を考えてみよう。少し離れた場所に住む友達と遊ぶ約束をしている。当日は電車で待ち合わせ場所に向かう。朝、身支度をしていると友達から「何時くらいに着きそう?」と連絡が入った。私は何と答えるだろうか。待ち合わせ場所が何度も行ったことのある駅であれば、電車の発車時刻をよく知っているから「40分後くらいかな」と到着予定時刻を見積ることができる。そしてその見積もりはほほ正確である。一方で行ったこともない場所で待ち合わせをする場合はどうだろうか。時刻表を調べて綿密な行動計画を立てていれば遅刻する可能性は減らせるかもしれないが予定通りにならないこともある。電車の到着が遅れるかもしれない。乗り継ぎがうまくいかず1時間近く遅れてしまうようなこともある。経験の少ないことについての見積もりは難しく不正確なのである。
システム開発も同様である。見積もりをしろと言われても、見積もりをする時点では実装が何時間でできるか――電車が予定の時刻に到着するか――について保証することはできない。あくまで過去の経験をもとに想像するだけである。その想像通りに事が進む確率はどのくらいだろうか。結果的に、私は「4週間あればなんとか終わるかな。でも不測の事態があるかもしれないから6週間と見積もることにしよう」という風にして見積もりを行っているのだ。その結果、思っていたより簡単で2週間で終わることもあれば、6週間経っても完成しないこともあった。
私がシステム開発をしてきた経験則では、1人で開発すれば6週間かかるという見積もりに対してそこに3人を投入するというのは「開発の相談相手がいることで開発がスムーズに進められたり、1人が病気で休むことになっても開発が止まらない」という安全な組織体制づくりの話であって、開発期間を短くするということには直接的には寄与しないと考えている。「いやいや、1人で6週間というなら3人もいたら4週間で終わらないはずはないだろう」と考える人がいるかもしれないが、そう考える人はパーキンソンの法則がなぜ生じるのかについて説明ができるだろうか。この世はそんなに単純なモデルでは表せられないのである。もっと言えば、1人より3人の方が作業効率が上がるとも言い切れない。この『人月の神話』でも言及されているブルックスの法則というものもある。人同士の相性もあれば、個々人の能力の差もある。そこが噛み合わなければ作業効率は下がる可能性すらある。
ここで話は変わるが、ペアプログラミングまたはモブプログラミングというものを知っているだろうか。それらのやり方は多少のバリエーションはあるが、役割を決めて複数人で1つの問題(タスク)に着手するというものである。「1人でできることを複数人でやるのは人的リソースの無駄だ」と思わないことが重要である。一見無駄なようにも思えてしまうが実際にやってみると想像以上に理解が促進し学習効果が得られるのである。モブプロの真髄を一度味わってしまうと別枠で勉強会を開催するのが馬鹿馬鹿しく思えてくるかもしれない。人と月を交換する話とは少し違うが、新人エンジニアが短期間で就職先の開発業務を理解する手段として効果的な手法なのでここで紹介しておきたくなった。モブプログラミングについては、次のブログ記事(並びにモブプログラミングアドベントカレンダー)が参考になる。
少し話が逸れてしまったが、話をまとめると、工数見積もりによって表現された情報は非常に単純化されたモデルであり、開発現場の実世界を表現しきれていないということである。このような不正確なモデルに頼って計画を立ててしまうから失敗してしまうのである。うまくいくのはたまたまなのである。工数はあくまで参考情報でしかない。Wikipediaと一緒である。信じてはいけない。
そもそも工数見積もりは必要なのかという議論もある。見積もりをすること自体は良いかもしれないが、どのような考えで見積もるのか、個人ではなくチームで見積もることはできないのか、工数とは別の指標で見積もれないかといったことを考えるのもよいのかもしれない。アジャイル開発やスクラムでは工数見積もりを行わずに作業計画を立てる方法も確立されていたりする。見積もりが難しいと感じたら、見積もりの仕方を考え直してもよいのかもしれない。
生きづらい世界でこの先生きのこるには
突如として物騒な見出し(注5)であるが、2020年現在を生きるいま、私は日本では色々なことがあったと感じる。そんなことを言ったら2019年だってそうだろうし、そうでない年なんてないのかもしれない。しかし「昔」よりも「今」が生きづらいと感じる要素が増えているように私は感じる。それが何であって、それを解決することはここでは目的ではないが、そのように感じる「今の日本」という世界は一体どのようにモデル化できるのだろうか。
(注5)朝から書き始めたこの記事だが、すでに今は深夜である。「この先生きのこる」は「この先、生き残る」であるが「この先生、キノコる」と誤読できることで一時期話題となった表現である。実はこのネタは2ちゃんねる発祥であり、2002年8月に土木・建築板に立てられたスレッドが元であるらしい。
生きていると理不尽な目に遭うことがある。さて、それは不幸なことだろうか。どの国に生きていても、いつの時代を生きていても理不尽な目に遭うことはあるだろう。「不幸な人は他にもいるのだから、自分が不幸なことを嘆くな」と言いたいわけではない。むしろ嘆くべきである。不幸なことを認識して、それを減らしていくその気持ちと行動が我々の人生を華やかなものにしてくれる。行動は正義である。
歴史上の人物として偉大な実績を残した有名な人の中にも、不憫な人生を送って生涯を終えた人がいる。その中でも私の好きな分野である数学史から3人を紹介したい。以下の話を記述するにあたっては飲茶氏の『哲学的な何か、あと数学とか』を大いに参考にし、引用もさせていただいた。
数学のお話
ソフィ・ジェルマン
1人目はソフィ・ジェルマン。1776年に生まれ1831年(55歳)まで生きたフランスの女性数学者である。
ソフィは、フェルマーの最終定理が発表されてから150年後にその難問に挑み実績を上げた数学者として知られている。彼女はフェルマーの最終定理がn=3,4の時のみしか証明されていなかった時代に「pと2p+1が奇素数であり、かつx,y,zのいずれもpと互いに素である場合に関しては、n=pでフェルマーの最終定理は正しい」ことを証明した。これは、n=3,5,7といった個別の数に対してしかアプローチできなかった状況において「x,y,zのいずれもpと互いに素」という条件付きではあるがpと2p+1が素数であるような数であれば常に成立することを証明した点において、フェルマーの最終定理の証明を大幅に進展させた偉大な業績である。
そんな彼女であるが、当時は「女性に学問は不要」とされていた差別と偏見の時代であり、彼女の母国フランスはその傾向が強かった。若き日のソフィは家族の反対に耐えながら隠れて数学を勉強していたが、大学入学という壁に阻まれてしまう。当時は入学できるのが男性のみであり女性の受験が認められていなかったのである。天才的な才能を持ちながら女性であるという理由で迫害されていたソフィは、以前大学に在籍していた男性の名前を騙って学校に潜り込むことを計画する。その計画は成功するが、そこで「彼」は数学の講義において優秀な実績を上げてしまう。講義を担当していた天才数学者ラグランジュは優秀な彼を呼び出してしまう。そこでソフィが女性であることがバレてしまうのだが、ラグランジュは彼女の素質を認め受け入れることを約束する。その後、彼女は物理学の世界でも実績を上げることとなる。しかし当時の科学界は女性科学者という存在に否定的でありソフィの実績に対して相応の評価をしていなかった。その状況に疑問を抱いた天才数学者ガウスはソフィに対して名誉を送ろうと働きかけるものの、その名誉を受け取る前に彼女は病気でこの世を去ってしまい名誉を受け取ることができなかった。というお話である。この出来事をきっかけに科学史において女性差別を行なっていたことが歴史上の「恥」であるという認識が広まることとなった。
ニールス・アーベル
2人目はニールス・アーベル。1802年に生まれ1829年(26歳)まで生きたノルウェーの数学者である。
16世紀の数学者は3次および4次の代数方程式の解の公式を探すのに必死になっていた。結果、16世紀の終わり頃には4次方程式までは解の公式が発見されるが、5次方程式のそれはいつまで経っても見つけられなかった。アーベルはその300年後の19世紀にノルウェーの小さな寒村で生まれた。アーベルは16歳のときに数学の面白さに取り憑かれてその才能に目覚め、数学を極めようと努力していたものの家が貧乏で大学に行くことができなかった。そんな彼は弱冠22歳にして「5次以上の代数方程式には一般的な解の公式が存在しない」という300年以上未解決であった問題の証明に成功する。が、しかし、その証明を有名な数学者に送る際に貧乏であったためきちんとした書類が用意できず、その数学者は重大な内容が記されたアーベルからの手紙を無視してしまうという出来事が起きてしまう。これには訳があった。当時は数学者宛にアマチュアからたくさんの手紙が届いていてそのほとんどが読むに値しない内容のものであった。貧乏なアーベルからの手紙は、読むに値しない手紙の中に紛れてしまったのである。
その後、アーベルは周囲の人々の協力もあり留学できる環境が整うこととなる。留学先で彼は数学を勉強しながら、改めて5次以上の方程式の解の公式に関する論文を学会に提出する。しかしこのとき論文を受け取った学会の審査員があろうことかアーベルの論文を紛失してしまい、紛失した事実ごと有耶無耶にされてしまう。アーベルは論文が紛失されたなどとは思っておらず査読結果を待っていたが、いつまで経っても返事がこない。ついには留学の期限も迫り、アーベルは自身の論文が却下されたのだろうと意気消沈し故郷に帰ってしまう。故郷に帰ってからは奨学金の返済など生活苦に追われ、とうとう身体も壊してしまう。そんな中、アーベルは最後の力を振り絞って留学中に出会った親友クレレを通じて三度目の論文提出を行う。その三度目の論文はようやく一流の数学者ヤコビの目にとまり、ヤコビはその論文の価値の大きさに気づく。クレレから事情を聞かされたヤコビは過去に二度もこの論文が無視されていたことに憤り、すぐさまアーベルを招致するように働きかけた。クレレはアーベルに手紙でそのことを伝え、ヤコビはアーベルが生活苦に困ることなく数学を続けられるような準備をしようとしていたところだったが、クレレからの手紙を受け取る数日前にアーベルは病気でこの世を去ってしまった。
エヴァリスト・ガロア
3人目はエヴァリスト・ガロア。1811年に生まれ1832年(20歳)まで生きたフランスの数学者である。ガロアもアーベルと同様に「5次以上の方程式の解の公式」に関する実績が有名であるが、ガロアは当時発見されていない数学上の新しい概念である「群論」を含む「ガロア理論」というアイデアを提唱した。この理論は21世紀の現代数学でも非常に重要な数学理論であり、19世紀当時に10代でその理論を提唱したことの実績は非常に高く評価されているが、その評価は彼の死後から何十年も経った後だった。
ガロアは存命中に前述の2人よりも不遇な人生を送っている。ガロアは16歳で数学に出会いそこから数学の才能に目覚める(そしてそれは当時の天才数学者と比べても群を抜いていた真の天才であった)のだが、数学にのめり込むあまり、彼は他人を信じられない性格になってしまった。真の天才には往々にしてそういう側面があるのかもしれない。数学の才能は十分であったものの、その性格のせいで数学を勉強するために受けたフランスの名門大学に落ちてしまう。翌年、ガロアはもう一度受験をするが、その大学は受験回数に2回までという制限があったためガロアにとっては最後のチャンスであった。しかし、ガロアが二度目の受験をする数日前に事件が起きてしまう。町長でありガロアが尊敬する父親が、町長の座を狙う司祭の陰謀によって無実の罪を着せられ自殺してしまうのである。ガロアは尊敬する父親を失ったショックで動揺し、二度目の受験で冷静にいることができず受験に失敗してしまう。しかしガロアは、父親を失っても大学に入れなくても自分には数学があると信じて、当時の数学者の間で話題となっていた「5次方程式の解の公式」について研究に没頭した。その中で生み出した「ガロア理論」についての論文を学会に提出したのだが、なんと学会はガロアの論文をアーベルの論文と同様に紛失してしまう。ガロアは再度学会に論文を送るが、今度は論文を受け取った数学者が病で急死してしまい結果として再び論文が紛失してしまう。それでもガロアは諦めずに三度目の論文を提出し、ようやく査読が行われることになったが、その査読結果はガロアの期待を完全に打ち砕くものであった。「ガロアの証明は、厳密でもなく、十分に展開されてもいないため審査できません」――これはガロアの論文に不備があったということではない。あまりにガロア理論が斬新すぎたが故に当時の数学者はその内容を理解できなかったのである。
信じていた数学をも否定されたガロアはついに心を閉ざしてしまう。当時のガロアの状況を知ったソフィ・ジェルマンは、ガロアについて「生意気だけれどもすぐれた才能を持つあの子は、このままでは狂ってしまいます……あれほどの才能を持つ若者がこのまま失われてしまうなんて……私はそれを恐れています」といった内容の手紙をソフィの知人に送っていたという。しかしながらソフィの想いも虚しく、父親も数学も奪われたガロアに残された道は過激な革命運動をすることであった。自暴自棄になり、自殺未遂までしてしまうほど狂ってしまっていた。そんなガロアにも最後に一つだけ残された希望があった。ガロアはある女性に恋をしたのだ。ガロアを立ち直らせてくれるかもしれない存在と巡り逢ったのだ。しかしガロアは最後まで不運であった。その女性には婚約者がいたのである。そしてガロアは彼女の婚約者から決闘を申し込まれることになる。ガロアは信頼できる友人に向けてこれまで自身が生み出した数学の理論を遺書として書き、「僕にはもう時間がない」という言葉を手紙に添えて決闘に向かったのだった。享年20歳であった。
生きづらさを感じたときに思うこと
「――なぜ私がこんな理不尽な目に遭わなければならないのか」と感じることがある。そんなとき、私はソフィ、アーベル、ガロアを始めとする歴史上の偉大な、そして不遇な人生を送った人物を思い浮かべる。「彼らに比べたら私の出来事なんて――」と冷静に落ち着く時間を与えてくれる。前章が長くなってしまったので省略したが、計算機科学の父として知られるアラン・チューリングも想像を絶するような不遇な人生を送った一人である(注6)。
(注6)アラン・チューリングに興味があれば、映画『イミテーション・ゲーム/エニグマと天才数学者の秘密』を観ることをお勧めする。Amazon Prime Videoでも配信されている。
これは私の主観であるが、今の日本は生きづらいと感じることがある。報道やニュースを見ると、国や政府が様々な場面で非合理的とも思える判断をしていたり、技術面ではLibrahack事件・Winny事件・Wizard Bible事件・アラートループ事件・Coinhive事件に見る理不尽とも思える解釈を目にしたり、はたまた年金問題や税金問題、最低賃金問題や生活の保障に関する問題もいろいろある。社会人としてより身近な話をすれば、賃貸住宅における敷金・原状回復トラブルや、所属する会社から残業代が支払われないといった問題もあるだろう。
生きづらいと感じてしまう要因は様々なものがある。ある問題においては当事者同士についてどちらか一方が悪い場合もあるが、またそれとは違った状況である場合もある。誰が悪いとも言えない状況とでも言おうか。これについての解釈やモデルをここで表現することは私自身の理解が十分でないこと、またそのモデル化が容易ではないために難しいのだが、私自身が気づき始めた解決のキーワードとして「多様性(Diversity; ダイバーシティ)」というものがあることを紹介したい。
このことについてどう説明すれば伝わるだろうか。ひとつは、「評価(解釈)は一次元的ではない」ということである。私が知っている人について「良い人」「悪い人」というグループに分類することはできない。(恋愛的ではなく)相性的な意味で「好きな人」「嫌いな人」というグループに分類することもできない。イメージ的には評価は二次元、あるいはより多次元なのである。少しだけ具体的に言うならば「良い面もあるけど悪い面もある」というような評価がほとんどかもしれない。ある軸に限定して一次元的な評価をすることは可能だが、結論としてのその人の総合的な評価を下すことはとても難しいと考えている。――全ての犯罪者は悪い人なのだろうか。
多様性を許容したモデル化
「物事を一次元的に評価してしまうと誤った結論を導くことがある」というのが最近の私の「生きづらさ」を解消するための考え方だと思っている。例えば会社で理不尽に感じる出来事があったら、それが起こった理由が何なのかを客観的に解釈しようと考える。ある面において「相手が悪い」と考えることはあるが、そうした場合でもその出来事の全体像の原因を考えるのである。もしかしたらその人は誰かに指示されて、あるいは誰かに理不尽な目に遭わされた結果としてそのように振舞っているのかもしれない。
電車を乗り降りするときに割り込みされることがあるかもしれない。満員電車で押しつぶされて他の乗客に自分が文句を言われるかもしれない。そんな時に理不尽な行動をしてきた人に怒りを覚えるのではなく、なぜそのような行動を取ってしまったのかを客観的に考えるのである。割り込みをした人は気分が悪くてトイレに急ぎたかったのかもしれない。文句を言ってきた人はデスマーチに巻き込まれていて正常な判断ができない状況だったのかもしれない。この世には様々な人がいると同時に、同じ人でも時と場合によって様々な状態になってしまうのである。
とにかく、何か理不尽に思ったり相手の考えが理解できなくてつらさを感じたときには、一次元的にではなく多次元的に捉えたり多様性という言葉を思い浮かべることで、より適切にその世界をモデル化できるのだと感じるようになった。
ここで突然ではあるが、「HSP(Highly Sensitive Person; ハイリー・センシティブ・パーソン)」という言葉を紹介したい。何の話なのかと思われるかもしれないが、この記事の執筆期限が迫っていて「僕にはもう時間がない」のである。話を着地させるためにこのキーワードをここで紹介させてほしい。
HSPとは何か。日本でHSPの認知を広めた『「気がつきすぎて疲れる」が驚くほどなくなる「繊細さん」の本』の著者である武田友紀さんのWebサイトに次のように書かれている。
HSPは、Highly Sensitive Personの略で、アメリカの心理学者・エレイン・アーロン博士が提唱した概念です。
アーロン博士はアメリカで数千人を対象にした調査を行い、繊細さは性格によるものではなく生まれ持った気質の可能性が高いこと、そして、「生まれつき繊細な人」が5人に1人の割合で存在することなどを発表しています。
繊細さんの特徴は「感じる力が強い」という一言に集約されます。
ひとの気持ち、場の雰囲気といった人間関係に関するものから、光や音、気温などの環境の変化など、「自分の外側にあるもの」はもちろん、体調や自分自身の気持ち、新しく思いついたアイデアなど「自分の内側で起きていること」もよく感じ取ります。
感じる力が強く、他の人が気づかないような小さなことにもよく気づくため
- まわりに不機嫌な人がいると緊張する
- 細かいところまで気づくため、仕事に時間がかかる
- 相手が気を悪くすると思うと断れない
- 疲れやすく、ストレスが体調に出やすい
などの悩みを抱えることがあります。
私は何をするにも、慎重で時間をかけて丁寧に行う性癖(注7)があると自覚している。そしてそれは時に私を苦痛にさせる要因にもなっている。なぜそんな「つらさ」を感じるのかと考えていたのだが、最近になってどうやら「HSP」という概念を導入することでうまく説明できるようなモデル化ができるということに気が付いた。
(注7)「性癖」という言葉に「性的」な意味があると考えている人がいるようだがそれは誤りである。
HSPとは「繊細な人」という説明があるが、特に注意したいのはこれが「病気」ではなく「タイプ」であるということである。血液型と一緒である。血液型で性格を語るのはナンセンスだが、人は「A型」「B型」「O型」「AB型」に分類される。そして自分が何型であるかは単なる事実に過ぎない。HSPと分類されるような「繊細な人」もいれば、そうではない「非繊細な人」もいるということをモデル化している。なお、HSPには他に「HSS型HSP」といったタイプもあると分類している。
人のタイプは多種多様である。社交的な人、人見知りな人。他人から批判されても何とも思わない人、他人から何かを言われるとずっと気にしてしまう人。怖い人、優しい人。甘いものが好きな人、苦手な人。コーヒーはブラックな人、そもそもコーヒーが飲めない人。お酒が好きな人、居酒屋に行くのも嫌な人。いろんな人がいる。
例えば「社会人なんだから飲み会くらい付き合えよ」という発言が上司から部下にあったとしたら、その上司はパワーハラスメントあるいはアルコールハラスメントを行ったとして相応の処分対象になる可能性が高いだろう。この例は納得しやすいと思うが、人見知りな人に「社会人なんだからもっと社交的にならないとダメだよ」と言ったとしたらどうだろうか。電話対応が苦手な新人社員に「社会人なんだから電話くらい取れなきゃダメだよ」と言うのはどうだろうか。それは問題ないだろうと考えた場合、アルコールが苦手な人に「社会人なんだからお酒の場に付き合わなきゃダメだよ」と言うのとは何が違うのだろうか。社会人としての常識とは何だろうか。
全ての人が不幸にならないようにするためには、不幸にならないようなモデルを考える必要がある。そのモデルを前提にすれば「アルコールが苦手な人(飲み会の場も苦手な人)を飲み会に誘うのはよくないな」と判断ができたり、「電話対応が苦手な人には、電話対応しなくてもよいような仕組みづくりを考えよう」と建設的な方向で解決策を検討できるようになる。しかしそのモデルを考え出すことは容易ではない。ルールであるから守らせるというと聞こえはいいが、それは一種の強要である。何を強要し、何を寛容とするべきかの判断が合理的に行える組織は、組織に属する全ての人を幸せにすることができると思っている。
こうした話を表面的に語るのは簡単だが、組織として、あるいは一人の人間として実際に考えていくことは決して簡単ではない。そのような状況で、実際に私が感じる「つらさ」がなぜ生じているのかをうまくモデル化できる「HSP」という概念があったということをこの場を借りて共有したいというのが、この記事で物騒な見出しを書いた理由である。
まとめ
この記事は「新人エンジニアにオススメする技術書」がテーマなので『人月の神話』をタイトルにしていますが、その本の紹介以外にも伝えたいことを散りばめてみました。時間のない中で文字数制限なしという記事を思いのままに書いていたらこのような文章になってしまいました。本文で触れた文献をまとめておきます。
- 人月の神話
- 新人の時期に読むと良いことがあるというものではないですが、プロジェクトの進行を管理する立場になったときにこの本の内容を理解しているとチームを幸せにできます。
- 本を購入するのが億劫な方は、本文でも紹介したブログ記事を読むことをお勧めします。第0回:人月の神話とはなんなのか?(解説編)|本気で読み解く”人月の神話”
- モブプログラミング・ベストプラクティス ソフトウェアの品質と生産性をチームで高める
- 本文でも紹介したモブプログラミングのよくある誤解 – モブプログラミング Advent Calendar 2018の著者の方の書籍です。
- 新人の時期からモブプログラミングを理解してチーム内で実践することができれば開発物への理解を短時間で深められると思います。私はモブプロはOJTの中でも最も効果的な手法だと考えています。
- 哲学的な何か、あと数学とか
- これは技術書ではありませんが、数学史にまつわる話が面白くまとめられている本です。著者の飲茶氏は他にも哲学書などいくつかの本を執筆していて非常に面白く読みやすいのが特長です。
- 興味があれば飲茶氏のWebサイトを覗いてみるのもよいかもしれません。哲学的な何か、あと科学とか
- 「気がつきすぎて疲れる」が驚くほどなくなる 「繊細さん」の本
- これも技術書ではありませんが、周りに気を使い過ぎて疲れてしまうというタイプの人が存在するということについて分析した心理学カテゴリの本です。
- 今日も明日も「いいこと」がみつかる 「繊細さん」の幸せリストという新刊もあります。
複数の本を紹介しましたが、私からこの記事を読んでいるあなたに「これは読んだ方がいい」とお薦めするものは正直なところありません。本は読めと言われて読むものではなく、自分が読みたいと思ったものを手に取るべきだと思っています。この記事に限らず、どこかで見たり聞いたりした本について、興味を持ったものがあれば購入して読んでみてほしいです。紙の本が好きな人もいれば電子書籍が好きな人もいます。自分が好きな媒体のものを購入するとよいでしょう。読みたいものを読むからこそ知識になり、あなた自身の考えと解釈がそこに生まれます。
プログラミング言語を覚えるにも優秀なエンジニアになるにも、最も大事なものは知的好奇心だと私は思います。勉強することが大事だと思うかもしれませんが勉強を苦痛なく行うためにはそれを楽しむ心が大切なのです。あなたの知的好奇心を信じて興味を持った本を手にとってほしいと切に思います。あなたの知的好奇心を広げるためにも、この記事では注釈も含めて技術以外のトピックにフォーカスしてみました。関心を持って調べること、その姿勢こそが新人エンジニアにとって最も必要とされる技術です。
物事を調べるために、時には質問をすることが必要です。上手な質問の仕方の心得を覚えておくことも優秀なエンジニアになるためには重要な要素であると私の経験則からお伝えしておきます。
この文献の存在を知っているだけでもあなたはエンジニアとして一歩、優秀になれるはずです。
あなたの知的好奇心が今後の人生に役立つ技術書や文献と出会えることを願って、この記事を締めくくりたいと思います。
今週は「IIJエンジニアがオススメする技術書」特集をお送りしています。
新人エンジニアの皆さんは是非参考にしてください。
他の記事はこちら[オススメ技術書]
また、みなさんもオススメする技術書がありましたらこちらでご紹介ください!
Twitterハッシュタグ:#オススメ技術書







