Beautiful Code
2024年12月03日 火曜日

【IIJ 2024 TECHアドベントカレンダー 12/3の記事です】
人生の長い間に亘ってプログラムを書いてきた. 最初は大学院生の時, 記憶装置のない加減乗算だけの計算機を作り, 紙テープから数値と計算の命令を読み入れ, 中間結果は一旦紙テープに書き出し, それをまた読み入れて計算を続けるという代物だったが, 初期のプログラミングの楽しさはあった.
やがて研究室で, 今から見るとままごとのような小規模の計算機を組立てると, 私はライブラリプログラムの整備に熱中した.
大学で講義する身分になると, 次々と多くの計算機, 多くのプログラミング言語と付き合うことになり, 自分でいろいろなプログラムを書く他, 学生諸君には「プログラミングほど楽しいものはない」と訴え続けた.
プログラムは, まずは考えた通りに動く, または仕様書通りに動けばよい. しかしどのプログラムでも段々と機能を追加したくなり, その場凌ぎで補修するから次々とぐちゃぐちゃになり, 後からの機能追加も大騒ぎになる. 計算機が変って別の言語用に書き直すと大体はすーっとは動かない.
時間とともに機能が増えるのは世の常だが, それでもプログラムは出来るだけ美しく書くべきだといわれる. プログラムが美しいということについて, 今回は考えてみる.
書画とか構造物の美しさの基準にも多くの説があろうが, プログラムの場合も大勢の満足する定義はさらに不可能かも知れない. プログラムをディスプレイに表示した時, 文字の塊ごとに色を変えるというほど単純ではない.
まずなんといっても, プログラムが確かに合っていそうだと分るのが大事である. 他人や他社にプログラムを真似されないように, 分りにくくして保護するという話もあるが, それは論外である. 美しいプログラムにはエレガントな証明と似たセンスが必要であろう.
エレガントな証明の例だ. 8単位×8単位の正方形の枠は, 64平方単位の面積があり, 畳のような2単位×1単位のドミノ32枚で覆えるが, その正方形の左下と右上の隅を1単位×1単位ずつ切り取った62平方単位の場所は, 31枚のドミノでは覆うことが出来ないことの証明に, 始めの正方形を, 単位の長さの白黒の市松模様に塗り分けると(下の図0), 両隅を切り落した形では, 切り落したのが, 共に白か共に黒かであり, 白と黒が同数でなくなり, 白黒1ずつのドミノでは蔽えない. QED.
プログラムを書くより前に, 問題の解き方が疑義がないほどに明瞭であり, そしてプログラムにはその解法が素直に反映されているのが大切である.
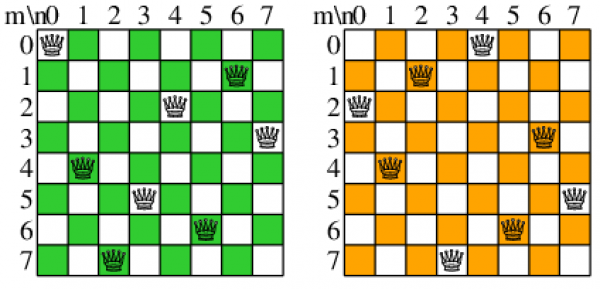
まずは情報科学標準問題といわれる「8クィーン(eight queens)問題」をやってみる. 8×8のチェス盤に8個のクィーンをどの2つも同一の行, 列, 斜め線の上にないような置き方は何通りあるか. その内2通りの置き方を図0に示す. 左のは, 左へ90°, 180°, 270°廻轉した置き方も条件を満すし, その夫々を左右反転しても条件を満すから, 同じ形の仲間は8通りある. 右のは180°廻轉すると元と同じになるので, 仲間は4通りある. 8通りの仲間は11種類, 4通りの仲間は1種類あって, 合計92通りの置き方がある.
議論のため, チェス盤の構造を定義しよう. 8×8の駒を置く場所をますといい, ますの横の並びを行(row), 縱の並びを列(column), 右上がりの斜め線を上向き(up), 右下がりの斜め線を下向き(down)という. 行は上から下へ, 列は左から右へ0から7と, 上向きは左上から右下へ, 下向きは左下から右上へ0から14と番号を付ける. 盤でのクィーンの置き方は, 列iでのクィーンの行番号の配列cで示す. 上の例はそれぞれ[0, 4, 7, 5, 2, 6, 1, 3], [2 , 4, 1, 7, 0, 6, 3, 5]だ. 同じ行, 同じ斜め線に2つ以上のクィーンがない条件は, 0 ≤ 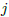 <
< 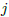 ′ < 8について,
′ < 8について, 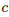
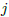 ≠
≠ 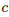
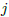 ′かつ|
′かつ| 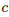
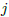 −
− 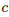
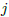 ′ |≠
′ |≠ 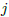 ′ −
′ − 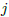 である.
である.
世の中にはモンテカルロ法があるとはいえ, チェス盤に8個のクィーンをランダムに置き, その内条件に合うものだけを数えるのはあまりにもばかげている. 行の番号は0から7まですべて現れるから, 条件の置き方は0, 1, · · · , 7の順列になるしかない.
そこでその順列を, 例えば2022年のこのIIJ Engineers Blogに私が書いた「Knuth: The Art of Computer Programmingの話」にある単純交換(plain change)のようなプログラムで生成し, 各々の順列について2つのクィーンが斜め線上にないなら出力するという方法はあり得る.
しかし列0の行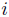 にクィーンを置くと, 列1ではもう行
にクィーンを置くと, 列1ではもう行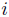 − 1,
− 1, 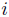 ,
, 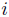 +1には置けないから, 次の列に置く時に置ける行だけから選ぶことにする. つまりクィーンを1個置いたら, そのクィーンから縱, 横, 斜めに置けないますに印をつけ, 各々の列では印のないますだけをクィーンを置いてみる位置の候補にする. 次のプログラムはそういう1例である.
+1には置けないから, 次の列に置く時に置ける行だけから選ぶことにする. つまりクィーンを1個置いたら, そのクィーンから縱, 横, 斜めに置けないますに印をつけ, 各々の列では印のないますだけをクィーンを置いてみる位置の候補にする. 次のプログラムはそういう1例である.
プログラム0 000 ups=[[0],[1,8],[2,9,16],[3,10,17,24],[4,11,18,25,32],[5,12,19,26,33,40], 001 [6,13,20,27,34,41,48],[7,14,21,28,35,42,49,56],[15,22,29,36,43,50,57], 002 [23,30,37,44,51,58],[31,38,45,52,59],[39,46,53,60],[47,54,61],[55,62], 003 [63]] #右上向き斜め線のアドレス 004 dns=[[7],[6,15],[5,14,23],[4,13,22,31],[3,12,21,30,39],[2,11,20,29,38,47], 005 [1,10,19,28,37,46,55],[0,9,18,27,36,45,54,63],[8,17,26,35,44,53,62], 006 [16,25,34,43,52,61],[24,33,42,51,60],[32,41,50,59],[40,49,58],[48,57], 007 [56]] #右下向き斜め線のアドレス 008 rws=[[0,8,16,24,32,40,48,56],[1,9,17,25,33,41,49,57],[2,10,18,26,34,42,50,58], 009 [3,11,19,27,35,43,51,59],[4,12,20,28,36,44,52,60], 010 [5,13,21,29,37,45,53,61],[6,14,22,30,38,46,54,62], 011 [7,15,23,31,39,47,55,63]] #行のアドレス 012 board=[0,1,2,3,4,5,6,7]*8 #盤には0...7を繰返し入れる 013 def test(m,board,ijs): 014 if m==8: print(ijs) #1つの解が得られ出力 015 else: 016 ns=list(filter(lambda n:n in range(0,8),board[m*8:(m+1)*8])) 017 for n in ns: #盤のm列で0から7の場所を選びnsとする 018 newboard=board[0:64] #コピーした新しい盤で置けなくなった場所に9を置く 019 for i in range(m*8,(m+1)*8): newboard[i]=9 020 for i in ups[m+n]: newboard[i]=9 021 for i in dns[n-m+7]: newboard[i]=9 022 for i in rws[n]: newboard[i]=9 023 test(m+1,newboard,ijs+[n]) #次の列でtestを呼ぶ 024 test(0,board,[])
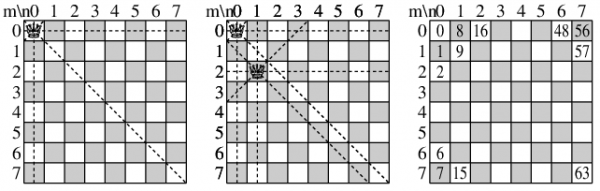
上のプログラムを説明しよう. 0行目のupsは上向き斜め線の通るますのアドレス, dns(downのこと)は下向き斜め線のそれである. 同じ行にも印をつけるためのアドレスがrwsである. boardはチェスの盤. ある列について, 印のない行番号が分るように, boardには各列ごとに上から0,1,· · · , 7を記入しておく. 置けないの印は0から7以外なら何の記号でもよいが, ここでは取り敢えず9にした.
13行目からクィーンを置く関数testである. 関数名はtryにしたいが, pythonではtryは予約語なので, testにした. 引数mはテストする列番号, boardは現在の盤, ijsはすでに置けたクィーンの位置のリストである. 14行目でmが8なら最後の列まで置けたので, ijsを出力する. そうでないなら(16行目), m列目から印でない, つまり0から7をfilter機能で選ぶ. それがこの列でクィーンの置ける行番号である. このリストをnsとする。
17行目. nsの値を順にnとして行nにクィーンを置く. そのクィーンによって置けなくなる位置は盤に印を付けるが, 印は複数のクィーンで付けた可能性があり, バックトラックの時に自分だけが付けた印を外すことが出来ないから, 現状の盤をコピーしてnewboardとし(18行目), それに印を付ける.
m列の作業中は, 印はm+1行目より右だけに付ければよいが, 一部にするのは面倒なので左側にも付ける. またm列は縱に付けるがこれは趣味の問題か. その後23行目でtestを再帰的に呼び出す.
これで92通りの置き方が, 小さい方から(辞書式順に)出力される. でも上向きや下向きの斜め線のますに全部印をつけるのはウンシャンだ. (ドイツ語unschön, 美しくない, 気に入らないこと) 斜め線1本につき1つの配列を都合2つ用意し, 置けなくなった斜め線はその対応するますに印を付ける. するともうそこに印を付けるクィーンはいないから, 印を付けたクィーンがバックトラックする時, 自分で印を外せばよい. 盤全体をコピーするより簡単明瞭である. 次はそういうプログラムを書こう.
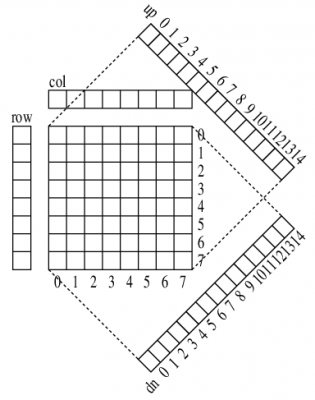
次の図で, 中央がチェス盤. これはプログラムでは使わない. その上の配列colは, その下の列のクィーンの位置の行番号を左から順に入れる. rowははその行にはまだクィーンが置けることをtrueで示す. upの配列はm列とn行にクィーンがまだ置ける時, m+nの上向き斜め線に対応する位置のtrueで示す. dnは下向き斜め線についてn−mの同様な配列である. ただ左下のm=7, n=0で, n−mは−7になり, 配列のアドレスは0からなので. n−m+7をアドレスにする.
プログラム1 000 cl = [none]*8 #各列のクィーンの位置 001 rw = [true]*8 #行にウィーンが置ける 002 up = [true]*15 #上向き斜め線にクィーンが置ける 003 dn = [true]*15 #下向き斜め線にクィーンが置ける 004 def col(m): #列mについてテスト 005 def row(n): #行nについてテスト 006 if n<8: 007 if rw[n] & up[m+n] & dn[n-m+7]: #まだ置けるか 008 cl[m]=n; rw[n]=up[m+n]=dn[n-m+7]=false #置けない印を付け 009 col(m+1) #次の列のテスト 010 dn[n-m+7]=up[m+n]=rw[n]=true; cl[m]=none #印を戻す 011 row(n+1) #次の行へ 012 if m<8: 013 row(0) #新しい列の行0から 014 else: 015 print(cl) 016 col(0)
配列rw, up, dnは, まだどこでも置けるから, 真(true)に初期化する(1,2,3行目). 関数colと関数rowを用意する. row(n)はnを0,1,· · ·,7と変えながら, 配列rw, up, dnを見てこのn行にクィーンが置けるか調べる. 置けるなら, cl[m]にnを記録し(8行目), rw, up, dnの対応位置を偽(false)にして次の列のcolを呼ぶ(9行目). colから戻ると, 先にfalseにした箇所を, 先程の逆順にtrueに戻す. 別に逆順の必要はないが, バックトラックの気分を出すためである.
この方式の8クィーン問題の解法は, O.-J.Dahl, E.W.Dijkstra, C.A.R.Hoare共著のStructured Programmingにあって, 標準的な解法とされれている.
この方法は, 前のクィーンの置けないますに印をつけるのより, 少しはスマートになった. しかし更なる改善はないか. 例えば配列upの代わりに, upでfalseの要素のインデックスの数列を使うのはどうか. upが[false,false,true,false,true,· · ·]のようなら, [0,1,3,· · ·]を使うのである. 帰る時に最後に追加したインデックスを外すのでもよいが, 引数にしよう. するとプログラムは以下のようになる.
プログラム2 000 def col(m, rw, up, dn): #列mについてテスト 001 def row(n): #行nについてテスト 002 if n<8: 003 if not((n in rw)or(m+n in up) or (m-n in dn)): #行nに置ける 004 col(m+1, rw+[n], up+[m+n], dn+[m-n]) #引数に置けない位置を追加 005 row(n+1) #次の行に進む 006 if m<8: #まだテストする列がある 007 row(0) #行0からテスト 008 else: 009 print(rw) #結果を出力 010 col(0, [], [], []) #列0からテスト 置けない位置の情報はまだない
これで8クィーンのプログラムは更に簡潔になった.
KnuthのTAOCP 7.2.2項の歴史的注によると, 19世紀の数学者, 天文学者のJohann Carl Friedrich Gauss (1777-1855)が8クィーン問題に興味を持ち, 友人への手紙にバックトラックの記載があるらしい. 8クィーンの置き方の12種類を初めて調べたのはGaussだそうである.
Gaussが8クィーン問題に興味を持った1850年の頃には計算機はないから, Gaussは手で計算した. 各列にあるクィーンの行位置の並びはもちろん0から7の順列である. その中に同一斜め線に複数のクィーンが存在するかのGaussの調べ方はこうだったらしい.
たとえばその配置が[2, 5, 0, 6, 3, 7, 4, 1]だったとする. Gaussはこれに列番号[0, 1, · · ·, 7]を足したり引いたりした.
結果の列に同じ数が重複すると, 同じ斜め線にクィーンがあることになる. 上の場合, 足した結果(左側)には2が2回あり, それに対応する2数は同じ右上向き線上にあり, 引いた結果(右側)には2が2回, −2も2回あり, そこでは同じ右下向きにあることが分る.
この方式による8クィーンのプログラムも書いた.
プログラム3 000 def test(ns): #nsは既に置いた位置の配列 001 if len(ns)==8: print(ns) #8個揃ったら出力 002 else: 003 st=[1,2,3,4,5,6,7][:len(ns)+1] #1から既に置いた数までの列(列番号に対応) 004 for n in range(0,8): #0,...,7について 005 if not((n in ns) or #すでにあるか 006 (n in list(map(lambda a, b:a+b,ns,st))) or #上向き斜め線にあるか 007 (n in list(map(lambda a, b:a-b,ns,st)))): #下向き斜め線にあるか 008 test([n]+ns) #置けるならその位置を追加して次の列のテスト 009 test([]) #何も置いてない引数でテスト開始
ほぼ同じ時代の数学者, Leonhard Euler(1707-1783)は裕福な家に生まれたが, Gaussの家は貧しかった. 「Gaussが自ら語るところによると, 母親はGaussの正確な誕生日を思い出すことが出来なかった. 母親はそれが昇天祭より3日前の水曜日であることを覚えているに過ぎなかった.」ということで, Gaussは自分の誕生日を知ろうとし, まず1777年の復活祭の日取り調べた. 復活祭の日取りは天体の動きによるように見えるが, 天体とは無関係で, ローマ法王庁の作った月齢表などから算出する. この諸表の代わりに復活祭の日取りを求める計算式を23歳のGaussは考案した. 復活祭の日取りを計算する式はGaussのものの他にも沢山ある.
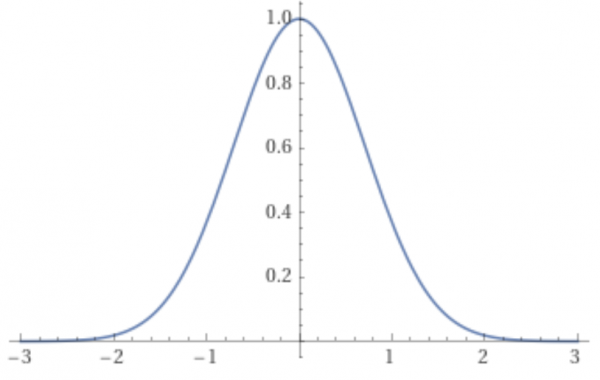
Euroになる前のドイツの10マルク紙幣にはGaussの肖像があった. 肖像の左には正規分布(Gauss分布)の曲線と, Gaussのいたゲッティンゲンの町の遠景が描かれている. 1998年8月にドイツであった国際会議に参加した後, かつて寺田寅彦などの物理学者, 正田建次郎などの数学者が若いころ留学したゲッティンゲン(昔の日本人は月沈原と書いた)へ行ってきた. 遊歩道の両側に菩提樹が生い茂る土手で市内は囲まれた落ち着いた学園都市である. 紙幣はコピーしてはいけないらしいが, 現役の紙幣ではないので(ついでにGauss分布も)お見せする. (英国の50ポンド紙幣の肖像はAlan Turingらしい.)
8クィーン問題はこのくらいにし, 次はソートが話題だ. 昔々の情報科学のシラバスではソートは必修項目であったが, 最近はどうであろうか. [3, 9, 0, 4, 2, 7, 8, 1, 6, 5]をソートするには, Pythonではsorted([3, 9, 0, 4, 2, 7, 8, 1, 6,5]), Schemeなら(sort ‘(3 9 0 4 2 7 8 1 6 5) <)の一発で得られる.
ソートも中々奥が深いが, 今回はその一隅をかすめるだけにしよう. ソートの最初はクィックソートである. 簡単にいえば, 小学生, 中学生, 高校生がごっちゃに1列に並んでいるのを学年順に並べ直すのに, 小学生だけ取り出す; それには低学年だけとりだすのように, 大雑把に分類しならがだんだんと精密にするようなものである.
例えば[3, 9, 0, 4, 2, 7, 8, 1, 6, 5]をクィックソートするには, 標準(ピボットという)として左端の3を取り, 3未満の列[0, 2,1]と3以上の列[9, 4, 7, 8, 6, 5]に分け, それぞれのクィックソートを長さ1の列になるまで繰り返すのである.
まず準備として, ごちゃごちゃの列を分割する情報科学標準問題のオランダ国旗の話から.
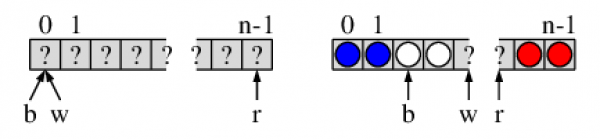
それぞれ任意個の赤, 白, 青のものが隠されてごちゃごちゃの順で1列に並んでいる. それを1要素を1回調べるだけで, 青を左端に, 赤を右端に, 白を中央に集めるプログラムを書く問題である. オランダ国旗は赤, 白, 青が上下だが, オランダ人のDijkstraがフランス人から聞いたといってこの問題を広めたので, 伝統的にオランダ国旗問題という.
この図の左は最初の状態を示す. 配列全体の長さをnとする. ポインタb, w, rを図のように初期化する. bはその左(b−1)より左側すべて(0まで)青であることを示す. wはその左(w−1) より左のbまで白が揃うことを示す. rはその右(r+1)から右端(n-1)まですべて赤であることを示す.
白の領域と赤の領域が出会うまで, 次を繰り返す. wの指すのが白ならwを1だけ右に寄せる. 赤ならrの指すものと交換し, rを1だけ左に寄せる. 青ならbの指すもの(白かも知れず, またb=wで今調べたものかも知れず)と交換し, bとwを1ずつ右に寄せる. プログラムにすると次のようだ.
プログラム4 000 def dutchflag(x): #赤,白,青の列をxとする. 001 def swap(i,j):x[i],x[j]=x[j],x[i] #iとjを交換 002 b=0;w=0;r=len(x)-1 #ポインtの初期化 003 while w<=r: 004 if x[w]=='red':swap(w,r);r=r-1 #赤ならwとrの先を交換 rから1引く 005 elif x[w]=='white':w=w+1 #白ならwに1足す 006 elif x[w]=='blue':swap(w,b);b=b+1;w=w+1 #青ならwとbの先を交換 wとbに1足す 007 return x #結果の列を返す 008 x=['blue','white','red','blue','white','red','blue','white','red'] 009 print(dutchflag(x))
これが分ればクィックソートは簡単だ. クィックソートする範囲の左端をleft, 右端をright とする. その範囲の左端の要素を比較の標準(ピボットp)とし, その右隣から右端までの要素の<pのものを左側へ, >pのものを右側に分離する. そして左の小さいもののソートとピボットと右の大きいもののソートを並べる.
大きいものと小さいものの分離は, オランダ国旗問題に似ているが, 通常は左からピボットより大きいものを探し, 右から小さいものを探し, 大きい方が左にあればこの両者を交換する.
そうだと思ってプログラムを見て欲しい.
プログラム5 000 def quicksort(ls): #配列lsをソートする 001 def qsort(left,right): #ソートする区域の左端と右端をleftとrightとする 002 if right-left>1: #まだソートする区域が2以上ある 003 p=ls[left];l=left+1;r=right #ピボットと左右のポインタの設定 004 while l<r: #ポインタが行過ぎていない 005 while ls[l]<p: l=l+1 #左がピボットより小lを増やす 006 while ls[r]>p: r=r-1 #右がピボットより大rを減らす 007 if l<r: ls[l],ls[r]=ls[r],ls[l] #大小逆転の交換 008 ls[left],ls[r]=ls[r],ls[left] #rの位置にピボットを移動 009 qsort(left,r-1);qsort(l,right) #両側のそれそれの区域をソート 010 qsort(0,len(ls)-1) #下請けを呼ぶ 011 return ls #ソート結果の区域全体を返す 012 print(quicksort([3,9,0,4,2,7,8,1,6,5]))
このプログラムquicksortには再帰的に呼ばれる下請け関数qsortがある. qsortはソートする区域の両端leftとrightを受け取るが, 区域の長さが0か1なら何もしない(2行目). 3行目でピボットpとポインタl, rを設定する. ポインタは両側から近付くが, 行き過ぎない内は, 右のポインタはピボットより小さいものを探し, 左のは大きいものを探す. 両者が探すものを見付けたら, lがrより左にあれば, lとrの指すものを交換する. 最終的には先程交換したものを再び見付けて停止する.
ピボットとの比較に等号がないのは, ピボットに等しいものはその場所に止めておいても無害だからである. 交換の回数を減らすために残しておく.
これで[3, 9, 0, 4, 2, 7, 8, 1, 6, 5]をクィックソートすると, 小さい方, ピボット, 大きい方は次のように変化する. 空リスト[]や長さ1の単項リストはそのままソートの結果となる.
A [3, 9, 0, 4, 2, 7, 8, 1, 6, 5] 1と9, 2と4を交換, ピボットが中央になるよう2と3を交換 B [2, 1, 0] 3 [4, 7, 8, 9, 6, 5] Aの結果の小さい方[2, 1, 0]をクィックソート C [0, 1] 2 [] Bの結果の[0, 1]をクィックソート D [] 0 [1] 空リスト, 数, 単項リストだけののでソート終了 E [] 4 [7, 8, 9, 6, 5] Aの結果の大きい方[4, 7, 8, 9, 6, 5]をクィックソ=ト E [6, 5] 7 [9, 8] Eの結果の小さい方[6, 5]をクィックソート G [5] 6 [] ソート終了 H [8] 9 [] ソート終了
ところでPythonにはフィルターの機能がある. それを使うとクィックソートはこんな感じになる.
プログラム6 000 def quicksort(ls): 001 if len(ls)<=1: return ls #長さが1以下なら何もしない 002 else: 003 p=ls[0] #左端をピボットにする 004 l=list(filter(lambda x:x<p,ls[1:])) #ピボット除く区域で小さいものを選ぶ 005 r=list(filter(lambda x:x>=p,ls[1:])) #同じ区域で大きいか等しいものを選ぶ 006 return quicksort(l)+[p]+quicksort(r) #上で選んだ区域をソートしピボットと繋ぐ 007 print(quicksort([3,9,0,4,2,7,8,1,6,5]))
たしかに簡潔だが, これではsortedと書くのとあまり違わず, プログラムをハックした気分にならない. この辺の線の引き方がむずかしい所だ.
クィックソートは英国人のC.A.R.Hoareが考案したといわれる. Hoareのことは皆がTonyと呼ぶが, AがAnthonyで, それがTonyになるらしい.
1996年にHappy Hacking Keyboard(HHKB)が市販されたしばらく後に, 私はオックスフォード大学に行く機会があった.
計算機科学科でTonyの教授室へ行き, HHKBを見せたら, Tonyは「これからは音声入力の時代だ」といって興味を示さなかった. スマートスピーカーで仕事をしている人なら兎に角, プログラムをハックするにはキーボードは必需品なのだが, Tonyはプログラミングへの興味を失ったのかな.
クィックソートも面白いが, ヒープソートもソートの方法としてはユニークだ. 従ってプログラムを考えるのも楽しい. ヒープソートは, 根に近いすべての階層に二進木のノードがあり, 最下段ではノードが左側から詰っている完全二進木で, 親のノードの値が左右の子のノードの値より大きい(小さくはないというべきか)データ構造を使う. これを最大ヒープ条件という. (後で述べるように最小ヒープもある.) この構造に根を0とし, 上から下, 左から右への順にアドレスを付ける. ノード0の子のアドレスが1と2, ノード1の子のアドレスが3と4だから, 親のノードのアドレスが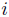 の時, 左の子のアドレスは2
の時, 左の子のアドレスは2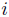 + 1, 右のは2
+ 1, 右のは2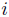 + 2である.
+ 2である.
親と子のノードがヒープ条件でない時, 2人の子の大きい方と親の値を交換する. 交換の結果親の値は増え, その親よりも大きくなるかも知れず, そうすると更に交換が生じる. これを篩い上げ(sift up)という. 一方, 子の値は減り, その子よりも小さくなるかも知れず, この場合も更に大きい方の子との交換が生じる. こちらは滴り落ち(tricle down)という.
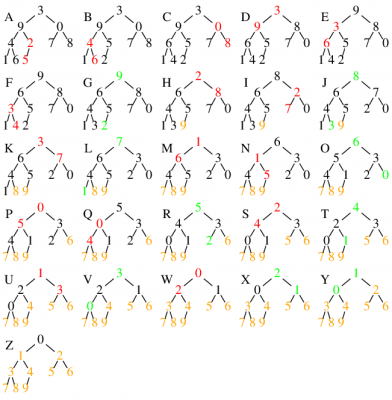
例によって[3, 9, 0, 4, 2, 7, 8, 1, 6, 5] をヒープソートする様子を図6の紙芝居で見よう. その図Aはソートすべき数列を, そのまま完全二分木に納めたところを示す. 3のアドレスは0, 9のアドレスは1, 0のアドレスは2, …, 5のアドレスは9である.
これを見ると, 根の3の子に9があったりするから, ヒープではない. 子を持つ最後のノードはアドレス4にある2だ. ここから出発して上のノードへと大小を揃えて篩い上げしヒープ条件に合うようにする. 今の場合, 子の値の方が大きいから, 2と5(アドレスでいえば, 4と9)を交換する. この図では, 将に交換しようとする要素を赤で示す. 繰り下がった2の場所には子がないから滴り落ちはせず, この交換は終り.
図Bで, 次に子を持つ親のノードはアドレスが1だけ少ないものだから, アドレス3の4と両方の子, アドレス7と8の1と6を比べ, 親の4と大きい方の子6(アドレスでいえば, 3と8)を交換する. 下がった4には子がないから交換は終り.
次の図Cで0と8を交換. 続いて親の9と子の6と5を比べるが, 親が大きいから何もしない.
図Dではアドレス0の3と両方の子の9と8を比べ, 3と子の大きい方9を交換する. この場合は下がった3がその子6と5より小さいから, 滴り落ち状態になり, その大きい方と6と交換になる(図E).
図Fでは, さらに下がった3は4より小さいので交換. その場所には子がないから滴り落ちはここで終わり, 二分木はヒープ条件を満した. そこで根にいる最大の9と, ヒープ木の末席にいる2と交換する(図G 交換するものは緑色).
9はこれで最終位置に着いたのでいわゆる殿堂入りし, 以後のソートには関らない. 図ではオレンジ色で示す. 一方最上段に出た2は, 本来いる位置ではないので, 滴り落ちが始まり, 子の6と8と比べられ, 大きい方の8と交換(図H), さらに下の7と交換して(図I)ヒープが完成し, 8と殿堂を除いた最後の3と交換して, 8も殿堂入りする(図J). 以後は図Kで3の滴り落ちが始まり, 図Lで7と1を交換. 図M, Nで1が滴り落ち, 6が殿堂入り. … 図Zで1も殿堂入りしてソートが終わる.
以上のソートの方式をプログラムにしたのがプログラム7だ.
プログラム7 000 def heapsort(ls): 001 n = len(ls) 002 def swap(i,j): #iとjを交換 003 ls[i],ls[j]=ls[j],ls[i] 004 def heap(i,r): #ノードiからr-1までの区間までのヒープを形成する 005 j0=2*i+1; j1=2*i+2; mx=i #iの左の子j0, 右の子j1 006 if j0 < r and ls[mx] < ls[j0]: #親と左の子を比べる 007 mx = j0 008 if j1 < r and ls[mx] < ls[j1]: #その大きい方と右の子を比べる 009 mx = j1 010 if mx != i: #いずれかの子が親より大きければ親子で交換し 011 swap(i, mx); heap(mx, r) #滴り落ちの処理 012 for i in range(n//2-1, -1, -1): #iを子のある最後のノードから0まで 013 heap(i, n) #篩い上げ 014 for r in range(n-1, 0, -1): 015 swap(0, r); heap(0, r) #根のノードを殿堂に入れ, 根から滴り落ち 016 return ls 017 print(heapsort([3,9,0,4,2,7,8,1,6,5]))
このソートは滴り落ちの方法が, 例えば親と子で値が2, 5, 4, 3, 1となっている時, 2と5を比較し, 右が大きいから2と5を交換, 次は2と4を比較し, 右が大きいから2と4を交換, 次は2と3を比較し交換する. いつも比較相手は2で, 2とそれより大きい値と交換する. それなら2をどこかに退けて置き, それと次々の値を比較して交換する条件の時は, 交換でなく親子の列で左へ移動する. 最後には移動した後に, 退けて置いた値を戻せばよいと思われる. aとbの交換は, Pythonならa,b=b,a と書けるが, 実際はaを退避し, bをaの場所に入れ, 退避の値をbの場所に入れるの3回の代入が必要だ.
しかし, 比較相手を退けて置く方式では, 毎回代入は1回である. KnuthのTAOCPにあるヒープソート(Algorithm523H)はそうなっているからそれを紹介する. ただ, TAOCPのプログラムはGoto文だらけで読み難いから, 以下のプログラム8は私が読み易いようPythonで書き直した.
プログラム8 000 def heapsort(ls): #lsをヒープソート 001 n = len(ls); l = n//2; r = n-1 #nは全体の長さlは子のある最後のノードrば最後のノード 002 while r > 0: #ソートする区間がある間 003 if l > 0: #篩い上げの途中なら 004 l = l-1; k = ls[l] #lを1減らしその値を基準とするkに置く 005 else: #篩い上げが終わっているなら 006 k = ls[r]; ls[r] = ls[0]; r = r-1 #最後を基準としてkに置くそこを殿堂にする 007 i = l #lから滴り落ちを始める 008 while i <= r: #殿堂の直前までのノードiについて 009 j = 2*i+1 #左の子をjとする 010 if j<r and ls[j]<ls[j+1]: #右の子がありその方が大きければ 011 j = j+1 #右の子をjとする 012 if j<=r and k<ls[j]: #子が殿堂より前で基準より大なら親の位置に入れる 013 ls[i] = ls[j]; i = j #滴り落ちを続ける 014 else: 015 ls[i] = k; i = r+1 #基準を空地に戻しソートの区間を縮める 016 return ls 017 print(heapsort([3,9,0,4,2,7,8,1,6,5]))
クィックソートをフィルタで大小の組に分けたように, ヒープソートでもPythonのライブラリheapq を使うことが出来る.
このプログラムは先に使ったヒープとは反対の最小ヒープを利用する. ソートしたい値を次々のheappushすると, 中に最小ヒープ木が構成され, heappopすると, 最小の値が返えされ, 残りの値で最小ピープ木が再構成される. ソートするにはこういうプログラムを書けばよい.
プログラム9 000 import heapq 001 def heapsort(ls): #lsをヒープソートする 002 h = [] #ヒープ木をhとする 003 for n in ls: #ソートする数をすべて 004 heapq.heappush(h, n) #heappushする 005 ls = [] #出力配列を用意 006 while h != []: #ヒープ木がある間 007 ls.append(heapq.heappop(h)) #heappopする 008 return ls #lsを返す 009 print(heapsort([3,9,0,4,2,7,8,1,6,5]))
[3,9,0,4,2,7,8,1,6,5]をヒープソートした時, データをpushするたびに, ヒープ木hが大きくなる様子(左側), popするたびに小くなる様子(右側)を下に示す.
[3] [1, 2, 3, 5, 4, 7, 8, 9, 6] [3, 9] [2, 4, 3, 5, 6, 7, 8, 9] [0, 9, 3] [3, 4, 7, 5, 6, 9, 8] [0, 4, 3, 9] [4, 5, 7, 8, 6, 9] [0, 2, 3, 9, 4] [5, 6, 7, 8, 9] [0, 2, 3, 9, 4, 7] [6, 8, 7, 9] [0, 2, 3, 9, 4, 7, 8] [7, 8, 9] [0, 1, 3, 2, 4, 7, 8, 9] [8, 9] [0, 1, 3, 2, 4, 7, 8, 9, 6] [9] [0, 1, 3, 2, 4, 7, 8, 9, 6, 5] []
8クィーン, クィックソート, ヒープソートのプログラムをいくつかお見せした. ご理解頂けただろうか. 「美」の定義が難しいように「プログラムの美しさ」も漠然としている. 私の考えでは, プログラムが美しいとは, 簡潔で構造が明解で. 理解し易いとほぼ同義である. 簡潔であるために, 効率の多少の低下は止むなしとする.
1968年にDijkstraが「Go To Statement Considered Harmful」をCommACMに寄稿した[0]. プログラムの質はGoto文の量の減少関数であり, 人間はこういう動的な構造は理解し難く, 将来の高水準プログラム言語からはGoto文は取り除くべきだと説いた.
SchemeやPythonにはGoto文がないから, プログラムの理解度改善には役立つ. 「ソフトウェア工学」論争たけなわの頃, 変数名の改善と段下げ(indent)の導入が, プログラムの理解へどう影響するかの実験をやった研究室もあった. 段下げは確かに有効で, Pythonでは段下げが違うと文句をいう. Schemeではプリティプリントすると構造が確認できる.
変数名は実体を表すように長くすると確かに分り易いが, それはそれで読み難くなる. 分り易く短か目の変数名を選ぶのはプログラマのセンスである.
新しいプログラムに取り掛かると, どうしても考え違い, 打ち違いなどで期待した出力がすぐには出ないことが多い. あちこち手直しするうちに, やっと期待した出力が得られると, 不思議や不思議, その途端にプログラムの構造が頭の中に鮮明に見えるようになる. そうすると, さらに適したプログラム構造やデータ構造のヒントが得られたりする. そうなれば, 最初の修正だらけのプログラムは気前よく放棄し, 新しくプログラムを書く. これは分り易いプログラムを書く1つの方法である.
しかし最終的な手段はプログラムを考えながら何度も見直し, 読み直し, 書き直すことである. 今回使ったプログラムはどれも何度も書き直しを繰り返した結果である.
プログラムを美しくと提唱する1人にKnuthがいる. Turing賞の受賞講演[1]で, “The chief goal of my work as educator and author is to help people learn how to write beautiful programs.” という. それにしてはTAOCPのアルゴリズムの分り難さは何か.
この講演の続きに, 美しさは「有用性(useful)」であるとも書いてあるが, それは違う. プログラムが分り易ければ使い易くもあろうが, 別に他人に使って貰わなくても美しいプログラムは書ける.
ANSI Common Listの序文の最後にPaul Grahamが書いた. “The spirit of Lisp hacking can be expressed in two sentences. Programming should be fun. Programs should be beautiful.” そう, それに尽きる.
参考文献
[0] Edsgar Dijkstra, Go To Statement Considered Harmful, CommACM, 13,3 (March,1968), pp.147-148,
https://homepages.cwi.nl/~storm/teaching/reader/Dijkstra68.pdf
[1] Donald E. Knuth, Computer Programming as an Art, CommACM, 17,12 (December,1974), pp.667-673,
https://paulgraham.com/knuth.html

Xのフォロー&条件付きツイートで、「IoT米」と「バリーくんシール」のセットを抽選でプレゼント!
応募期間は2024/12/02~2024/12/31まで。詳細はこちらをご覧ください。
今すぐポストするならこちら→![]() フォローもお忘れなく!
フォローもお忘れなく!



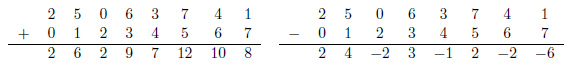

![「たのしいぱそこん [My First Internet ~はじめてインターネットに触れたとき~]」のイメージ](https://eng-blog.iij.ad.jp/wp-content/uploads/2022/11/e4d8bc4091624cf1e8cccc76ed34a706-300x169.jpg)