パラメトロン

【IIJ 2025 TECHアドベントカレンダー 12/23の記事です】

2025年11月27日パラメトロンに授与されたIEEEマイルストーン銘板
東大理学部1号館に掲示された

私は漫画やコミックにはうといので, 正確ではないかもしれないが, 少年ジャンプのDr.STONEでパラメトロンが話題になったそうだ. 崩壊した文明を復興させるのに, 計算機が必要であり, トランジスタは高精細な製造装置が必要なのに対し,パラメトロンなら鉄粉を焼き固めてフェライトコアを作り. それに電線を卷いてコイルにして演算素子が作れ, 計算機が得られるという話らしい.
アメリカの電子情報学会ともいうべきIEEEは, 電気電子情報などの関連分野での歴史的偉業に対して, マイルストーンという銘板を授与して表彰するが, 本年(2025年)はパラメトロンもマイルストーンに認定され, 11月27日, 東京大学で, 藤井総長も出席して銘板授与式があった. (申請書はhttps://ieeemilestones.ethw.org/Milestone-Proposal:Parametron, 1954)
パラメトロンは70年ほど前の1954年に発明され, 1960年代まで使われたが, その後は殆んど忘れられているので, マイルストーンの機会に説明してみたい.
1950年頃, 日本でもそろそろ電子計算機が欲しいという機運になった. その原動力は英国ケンブリッジ大学で作られた計算機EDSACのチームが, 計算機の使い方についての本を出版したことにある. Maurice Wilkes他著, The Preparation of Programs for an Electronic Digital Computerで, EDSACのアーキテクチャ, プログラムライブラリ, プログラムの構成法, エラーの見付け方などが記述され, この本を解読した人は, 計算機の面白さに魅了され, 自分達の使える計算機が欲しいと思うようになった.この本はhttps://archive.org/details/programsforelect00wilk/mode/2upで見ることが出来る.
当時, 東大では, 工学部が文部省の予算を貰い, 東芝と共同で真空管式の計算機を建設中であったが難航していた. その頃院生であった私のいた理学部物理学科の高橋研でも, 自分達の計算機が欲しくなり, 工夫を重ねていた.
一つの研究室の予算では, 真空管やトランジスタの計算機を作るのは問題外であった. 真空管は電力が馬鹿にならないし, 暫く使うと電子の放出が減少し, 交換することになる. トランジスタは1個5000円, ダイオードは200円という時代である. 私が学部生のころの国立大学の授業料は年額3600円だったから, トランジスタはそれより高価だった.
高橋研では安い部品で計算機を作る方法を工夫し, 演算装置に廃品の電話交換機のリレー, 記憶装置にコンデンサーを使う機械電子式を考え, 一部試作もしたらしいが, いかにも遲そうである. その内, 私より少し上の大学院生の後藤英一さんが, フェライトコアのコイルとコンデンサーの回路をパラメータ励振した素子が使えるのではないかと気付く.
後藤さんは高校生の頃から電子回路に精通し, テレビ受像機を試作して試験放送を受信したり, フェライトコアを利用したスィープジェネレータを考案して波形を楽しんだりしたそうだ. その電子工作力と, 後から分ったことだが, 使ったフェライトコアの性質が適していたこととで, パラメータ励振回路はすぐに完成し, 3拍励振法も開発して演算素子が出来上った.1954年春のことである. 素子はパラメトロンと命名された.
次にパラメトロンの仕掛けを説明しよう.
インダクタンスヘンリーのコイルとキャパシタンスファラッドのコンデンサーを直列に継ぐと共振回路が作れる. その共振周波数, 秒⁻¹は, = である. これの次元は, コイルを流れる電流とコンデンサーに掛る電圧の関係が
　だから次元としては　
従っての次元はである.
この共振回路のパラメータ励振というのは, 共振周波数を決めるパラメータ, を共振周波数の2倍, つまり2で変えることである. パラメトロンでは, コイルの中にフェライトコアを入れ, そこに2の交流とバイアスの直流を足したものを流す. するとが2で変化し, 共振が増幅されるのである.
もっとも身近かなパラメータ励振は, 公園や遊園地にあるブランコである. ブランコは振り子の一種であり, その振り子は,支点から重心までの長さm, 重力加速度m秒⁻²の時, 周期(周波数の逆数)秒は, = 2πとなる. 公園などにあるブランコのは支点から子供の重心までの距離で, 子供がブランコの上で立ったりしゃがんだり(沈んだり)すると, は変化する.
例えばブランコが南北に揺れるとする. ブランコが最も南側から北へ向って動き始めた時, 子供は身体を低く沈め, 最も下を通ると今度は立ち上がってブランコは北側に着く. 反対に北から南へ揺れる時も, 始めから最も下までは沈み, 後半は立つ.
つまり, ブランコの1周期, 南から北へ行って南へ戻る間に, 子供は2回沈んで立つ. だから振り子の糸の長さは2回延びて縮むわけで, これが結局パラメータ励振でブランコの振幅を増加するわけである.
次の図で, 黒は励振電流を, 赤と青は共振回路の振動を示す. 共振の片方に対して他方はπだけ位相がずれているから, この2種類の振動を0相, π相といって区別する. 励振を始めた時, 共振回路が発振する位相は, 共振回路にあった微小な振動の位相による. 従ってある共振回路を望みの位相で発振させるには, すでに発振している共振回路から種子たねの振動を, トランスを経由して入れておけばよい.

パラメトロンの励振(黒線)と発振(赤と青の鎖線)

1個のパラメトロンは下の図のような構造である. 共振回路のコイルは励振電流の漏洩の影響を打ち消すように2個で出来ていて, 励振電流は逆に流れる仕掛けである. 左端の結合トランスは, 励振が掛る前に, 共振回路を0相(0)かπ相(1)のいずれにするかの種子を入れるためのもの, 右端の端子は後段の共振回路に種子の位相を伝えるためのものである.

1個のパラメトロンの構造

そこで, パラメトロンでは, 共振回路を3つのグループ, Phase I,II,IIIに分け, 夫々のグループを順に少しずつ重複するよう巡回させて励振し, 休止する. すると, Iのパラメトロンが共振している₁から₄の間に, その共振の位相が, IIのパラメトロンに伝わり, ₃でIIの励振が始まると, IIのパラメトロンがIから引き継いだ位相で発振する. IIがIIIに, IIIがIに伝わるというふうに伝搬し, 情報が維持される.

パラメトロンの3拍励振

パラメトロンの出力の上の端子から出た線が, 次のパラメトロンの結合トランスに紙の上から下に通り, 下の端子に戻る時(これを順方向ということにする), 両方のパラメトロンが同じ位相で発振するとする.
反対に上の端子から出て結合トランスを下から上へ通り下の端子へ戻る配線もあり得て(これを逆方向ということにする), その時は前のパラメトロンに対して後のパラメトロンは反対の位相で発振する.
この図ではPhase IからPhase IIへも, IIからIIIへも, IIIから1へも順方向に描けているから, すべてのパラメトロンは励振されると同じ位相で発振する. 但しこれだけでは, それが0相かπ相かは分らない. こういう接続を右のように描く.

3個のパラメトロンで情報を循環させる

次の図は, Phase Iの3個のパラメトロンがIIのパラメトロンに種子を入れるところである. よくよく眺めると, Iの上の2個からは順方向に接続するよう描いてあるが, 一番下からは逆方向に接続してある. こういう時には右のように, 逆方向の入力には線に交差する線分を追加して逆方向であることを示す. 順方向が多数だからIIは順方向に発振する.

奇数個のパラメトロンからの位相の情報の多数決で発振の位相が決まる

パラメトロンの写真などは, 情報処理学会コンピュータ博物館の
「パラメトロン」https://museum.ipsj.or.jp/computer/dawn/0007.html,
「PC-1 パラメトロン式計算機」https://museum.ipsj.or.jp/computer/dawn/0016.html
で見ることが出来る.
ここからはパラメトロン回路での論理演算, つまり多数決論理の話である. KnuthのThe Art of Computer Programmingの第4A巻では, 多数決とはいわず, 中央値medianという. 3項演算はと書く. Knuthによると, 「全宇宙の中でおそらくもっとも重要な演算」である.
多数決ではなく中央値というのは, 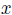≤ ≤ 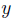の時(値の順に並べた時) = 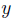と中央のものになるからだ.
最小限, 最大限という言葉からの類推で, 竹内郁雄君は, 最中限という言葉を発案し, トランプを使ったゲームを提案した. それについてはウィキペディアをご覧あれ. 最中限は止めて, 訳書では中央値にしているが, ここではやはり多数決を使う.
例えば2論理変数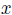, 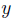の論理積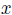 ∧ 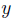は, 偶数個数の入力では多数決はとれないから, もう1個の常に偽(0)であるようなさくらの入力を追加する. すると下の真理値表の左端のように論理積が得られる. 0の列がさくらである. それに対応するパラメトロン回路はすぐ下にある通りである. 定数0の入力の代わりに円の中に-を, 1には+を書く.
論理和もまったく同様に実現出来る.
その次の2変数論理関数の例は, 左から三番目の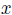 ⊃ 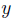で, これは含意とかimplicationといい, 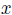⇒ 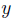と書く. 矢印から察せられるように, 「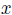なら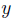」なのだが, 数学者にはこれで十分でも, もう少し詳しくいうと, 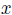が真の時は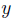の真理値が結果; 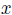が偽の時は, 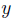に関係なく真ということだ. この後半はで前半は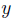だから, 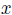⊃ 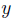= ∨ 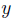と書いたりする. 主要な演算は∨だから,さくらは1. また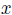の方は否定すればいいから, 真理値表は示す通り.
最後は排他的論理和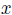 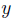で, これは多数決1段では実現できない. その理由は3変数の例のところで説明しよう.

排他的論理和は二進法の2数の同じ桁同士の加算に使われるが, この桁には下からの繰上げもあり得るから, 3変数の和が実現出来ればありがたい. 3入力が普通のパラメトロン向きというべきであろう.
下の図の左のパラメトロン回路が, 足し合せる2数のその桁のビットと, 下の桁からの繰上げのビットを足し, その桁の和と,上の桁への繰上げを出す全加算器である. これを考えた山田博さんの名を使って, 山田の回路ということがある. 3入力は同等なので, a, b, cを入力としよう. それを次の段のパラメトロンに入れ, d, e, fから中間出力が得られ, 更にそれを次の段のパラメトロンに入れると, この桁の和がパラメトロンgから得られ, 繰上げは中間結果のfから得られる.

3変数の全加算器

その説明が右にある7個の立方体図A, B, . . ., Gで, これは0, 1だけの三次元の様子を示す. 3変数の0, 1に対応する8箇所は,左端の図Aでの, 0 から7と記す頂点で示す. 説明の都合で, 各頂点には図Aのように番号をつけた. 図Bは変数a, b, cの値0,1について, 多数決の結果が1になる頂点を黒丸, 0のを白丸で示す. 全加算器では, これは上の桁への繰上げになる.
繰上げが1になる黒丸の頂点は, 図Bに見るように, 3,5,6,7で, これで分るように, 黒丸同士は, 途中に白丸を経由せずに辺で接続している. 反対に白丸同士も隣合い, 結果的には白と黒はそれぞれ一団になっている. その中間には破線のように境界が描ける. 多数決関数1段で実現出来るのは, この図のように, 白と黒が完全に分離している時である.
一方, 図Cは, 3変数の排他的論理和を示す. この図では辺を伝わって黒から黒へ, または白から白へ行こうとしても, 途中に他の色が存在し, 白同士, 黒同士の集団になっていない. だから多数決1段では実現出来ない.
右の残りの立方体はこれで全加算器が出来る説明である. 図Cは目標の全加算器の桁の和の結果(目標)である. 図Dはパラメトロンdの出力で, Bとほぼ同じだが, bが否定なので, 図Bの頂点0,1,4,5と2,3,6,7が入れ替わっている. 図Eはbが1の2,3,6,7だけが黒丸. Fはgに入るfの出力の否定で, Bと白黒が反対になる. D,E,Fの多数決がCである.
図Gは, D,E,Fの各頂点の黒丸の総和を示し, それは1か2であって, 0と3がないのに注目しよう. つまり常に2本の入力は消し合い, パラメトロンgは, 実質的には1入力と同じであり, ここに更に2入力を加えてゲートとなり得る.
3変数の排他的論理和が1段の多数決では得られず, 2段必要なことは分ったが, 任意の奇数の論理変数があっても, 多数決2段で排他的論理和が得られると, KnuthはTAOCPに書く. 3個を越える入力はパラメトロンとしては心配で使えないが, 数学的には考えられる.
＞ 0について, 2 + 1個の変数の排他的論理和は, 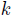＞= 1について, がと同じと考えるなら,

として,

である. この恐しい式を考えたのは, 高橋研によく現れては議論していた院生佐々木不可止君である. = 1の時は3入力の全加算器の和は得られるが, 山田の加算器のような繰上げの得られないのが難点である.
さらにパラメトロンの個数の多い回路も示す. 下の図の左上は4個のプリップフロップが並んだ二進カウンタである. 捻れているが, 各段の3個のパラメトロンでできたフリップフロップは+のパラメトロンのところでセット. -のところでリセットされる. inから入力があると, 最上段がセットされ, 次のinの入力でそれがリセットされて, 2段目がセットされる. 15個の入力ですべてがセット状態になり, その次の入力ですべてがリセットされ, cから出力がある.
左の下は全加算器4個の4桁の加算回路である. 最下桁の加算器への繰上げ入力C_inは, 減算の時に使う. しかしこの方式だと,繰上げが各桁毎に遅れるので, 右に示すような高速桁上げ回路が考えられた. 全加算器は右側に揃って置かれ, 左側に対数時間で桁上げを算出する回路がある.
例えばa₃とb₃を足して, その桁の和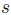₃を出す全加算器に入力される繰上げを見ると, a₂, b₂の入力は襷掛けになって次の2個のパラメトロンに入るから, a₂, b₂が0,0か1,1の時は, 繰上げも0か1になる. a₂, b₂が0,1か1,0だと打ち消し合い, a₁, b₁に依存することになる. a₁, b₁が0,0か1,1ならそれで繰上げは決まる. しかしこれも0,1か1,0だとすると, 打ち消すから, a₀, b₀, c_inで決まる繰上げが使われることになる.

パラメトロンを使った計算機PC-1(Parametron Computer One)は, 1957年9月に研究室内で組立てを始め, 翌1958年3月26日に動き始めた. その時はまだ乗除算命令はなかったが, 5月末には乗算, 7月末には除算の回路が追加され, 計算機として使えるようになり, 当時国産では最速の計算機として, 研究室で使わない時には学内に使用を公開していた.
1964年5月に, 学生が五月祭の展示に電源を借りたいといって, PC-1の電源を外して使ったが, 床の配線が複雑になっていて電源をどこに戻すか分らなくなった. その頃はPC-1の後継機富士通製のPC-2が使えるようになり, 研究室は次の研究の場所も必要ということで, それを機会にPC-1は運転を中止した.
PC-1は廃棄されたが, それより遥かに高速なシミュレータが私のMacBook で動く. 私の他にもPC-1シミュレータを作った人もいるらしい. なにしろアーキテクチャが簡単だから, シミュレータはすぐにも作れる. またたまにはパラメータ励振に成功したというニュースも屆くことがある.
一方世の中ではトランジスタの集積度や演算速度が向上し, 交流を使うパラメトロンは速度を上げるのが困難であって, 徐々に使われなくなった.
今では演算回路, 制御回路, 記憶装置は集積チップの中に収まってブラックボックスになり, その中身のことは何も分らない.
ブラックボックス化は電子回路に限らず, 車のエンジンもそうで, 内側はまったく分らなくなった. 1960年代に私が持っていたフォルクスワーゲン(かぶと虫)では, エンジンも小学生の頃に子供の科学で読んだ構造そのものだったが, 最近の車は何も見えない. そういう意味では60年前の計算機はなんでも分かり, なんでも出来て面白かった. そういう時代が懐しい. 古きよき時代であった.